题目内容
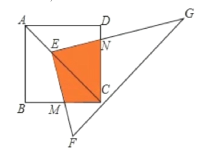
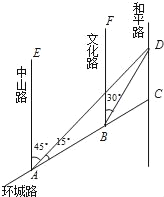
【题目】如图，AC是某市环城路的一段，AE，BF，CD都是南北方向的街道，其与环城路AC的交叉路口分别是A，B，C．经测量花卉世界D位于点A的北偏东45°方向，点B的北偏东30°方向上，AB=2km，∠DAC=15°．
（1）求B，D之间的距离；
（2）求C，D之间的距离．
【答案】（1）BD之间的距离为2km；（2）C，D之间的距离
km．
【解析】分析：（1）根据平行线的性质，以及方向角的定义即可求出
根据等角对等边，即可证得
即可求解；
（2）根据等角对等边即可证得
然后根据三角函数即可求得
的长．
详解：（1）如图，由题意得，
∴
∵AE∥BF∥CD，
∴
∵
∴
又∵
∴
．
∴
∴
为等腰三角形，
∴
即BD之间的距离为2km．
（2）过B作
，交其延长线于点O，
在
中，
∴
在
中，
∴
（km）．
即C，D之间的距离km．
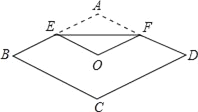
【题目】某班“数学兴趣小组”对函数
的图象和性质进行了探究，过程如下，请补充完整.
（1）自变量
的取值范围是全体实数，与
的几组对应值列表如下：
| … |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | … |
其中，
__________.
（2）根据上表的数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.
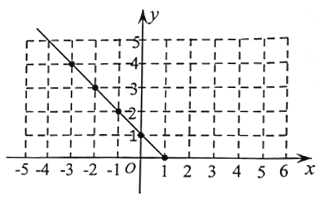
（3）观察图象，写出该函数的两条性质：
①____________________________________________________________
②____________________________________________________________
（4）进一步探究函数图象发现：
①方程
的解是__________.
②方程
的解是__________.
③关于的方程
有两个不相等实数根，则
的取值范围是__________.
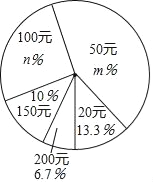
【题目】某中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现抽查了九年级（1）班全班同学捐款情况，并绘制出如下的统计表和统计图：
捐款（元） | 20 | 50 | 100 | 150 | 200 |
人数（人） | 4 | 12 | 9 | 3 | 2 |
求：（Ⅰ）m=_____，n=_____；
（Ⅱ）求学生捐款数目的众数、中位数和平均数；
（Ⅲ）若该校有学生2500人，估计该校学生共捐款多少元？
