Question

【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为6,则重叠部分四边形EMCN的面积为( )

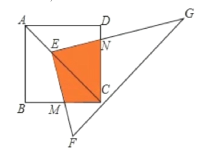
A. 9B. 12C. 16D. 32

Answer 1

【答案】C

【解析】

过E作EP⊥BC于点P，EQ⊥CD于点Q，△EPM≌△EQN，利用四边形EMCN的面积等于正方形PCQE的面积求解．

过E作EP⊥BC于点P，EQ⊥CD于点Q，

∵四边形ABCD是正方形，

∴∠BCD=90°，

又∵∠EPM=∠EQN=90°，

∴∠PEQ=90°，

∴∠PEM+∠MEQ=90°，

∵三角形FEG是直角三角形，

∴∠NEF=∠NEQ+∠MEQ=90°，

∴∠PEM=∠NEQ，

∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°，

∴EP=EQ，四边形PCQE是正方形，

在△EPM和△EQN中，

，

∴△EPM≌△EQN(ASA)

∴S△EQN=S△EPM，

∴四边形EMCN的面积等于正方形PCQE的面积，

∵正方形ABCD的边长为6，

∴AC=6，

∵EC=2AE，

∴EC=4，

∴EP=PC=4，

∴正方形PCQE的面积=4×4=16，

∴四边形EMCN的面积=16，

故选C