题目内容
If x，y and z are positive numbers such that 2x2-6y2+z2=0，6x2-2y2-z2=0，then the value of| x2-xz+z2 | x2+yz+y2 |
分析：根据2x2-6y2+z2=0，6x2-2y2-z2=0，x，y，z是正数，?x=y，z=2y，代入所求分式即可得出答案．
解答：解：由x，y，z是正数，2x2-6y2+z2=0，6x2-2y2-z2=0，
两式相加得出x=y，
把x=y代入2x2-6y2+z2=0，
解得：z=2y，
把x=y，z=2y代入
=
=
．
故答案为：
．
两式相加得出x=y，
把x=y代入2x2-6y2+z2=0，
解得：z=2y，
把x=y，z=2y代入
| x2-xz+z2 |
| x2+yz+y2 |
| y2-2y2+4y2 |
| y2+ 2y2+y2 |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查了分式的化简求值，难度不大，关键是根据已知条件用y把x与z表示出来后再代入求值．
练习册系列答案
阅读快车系列答案
相关题目
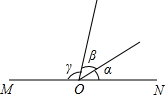In the figure 5，MON is a atyaight line，If the angles α、βandγ，satisfy β：α=2：1，andγ：β=3：1，then the angle β=
As in figure 2．In the circular ring of which center is point O．if AO⊥BO，and the area of the shadowy part is 25cm2，then the area of the circuiar ring equals to（ ） （π≈3.14）