题目内容
As in figure 2．In the circular ring of which center is point O．if AO⊥BO，and the area of the shadowy part is 25cm2，then the area of the circuiar ring equals to（ ） （π≈3.14）分析：设大圆的半径为R，小圆的半径为r，根据阴影的面积为两个直角三角形的面积之差，可得R2-r2=50，又知圆环的面积为两个圆的面积之差，据此即可解得答案．
解答：解：设大圆的半径为R，小圆的半径为r，
∵AO⊥BO，
∴阴影的面积为两个直角三角形的面积之差，
∴R2-r2=50，
∵圆环的面积为两个圆的面积之差，
∴圆环的面积=π（R2-r2）=50π=157cm2．
故选B．
∵AO⊥BO，
∴阴影的面积为两个直角三角形的面积之差，
∴R2-r2=50，
∵圆环的面积为两个圆的面积之差，
∴圆环的面积=π（R2-r2）=50π=157cm2．
故选B．
点评：本题主要考查面积及等积变换的知识点，首先根据阴影的面积求出两个圆的半径之间的关系，然后计算圆环的面积，本题解答比较巧．
练习册系列答案
相关题目
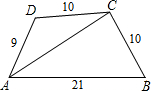As in right figure，in a quadrilateral ABCD，we have its diagonal AC bisects∠DAB，and AB=21，AD=9，BC=DC=10，then the distance from point C to line AB is
As in figure，the area of square ABCD is 169cm2 and the area ofthombus BCPQ is 156cm2．Then the area of the shadow part is（英汉词典：square正方形；thombus菱形）