题目内容
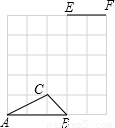
(2009•宝山区一模)如图,一条细绳系着一个小球在平面内摆动、已知细绳的长度为20厘米,当小球摆动到最高位置时,细绳偏转的角度为28°,那么小球在最高位置与最低位置时的高度差为 厘米(用所给数据表示即可).
【答案】分析:当小球在最高位置时,过小球作小球位置最低时细绳的垂线,在构建的直角三角形中,可根据偏转角的度数和细绳的长度,求出小球最低位置时的铅直高度,进而可求出小球在最高位置与最低位置时的高度差.
解答: 解:如图:过A作AB⊥OC于B.
解:如图:过A作AB⊥OC于B.
Rt△OAB中,OA=20厘米,∠AOB=28°,
∴OB=OA•cos28°=20×cos28°.
∴BC=OC-OB=20-20×cos28°=20(1-cos28°).
点评:此题考查了三角函数的基本概念,主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.
解答:
 解:如图:过A作AB⊥OC于B.
解:如图:过A作AB⊥OC于B.Rt△OAB中,OA=20厘米,∠AOB=28°,
∴OB=OA•cos28°=20×cos28°.
∴BC=OC-OB=20-20×cos28°=20(1-cos28°).
点评:此题考查了三角函数的基本概念,主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
(2009•宝山区一模)“三聚氰胺事件”对奶制品行业影响很大.为应对该事件对行业的冲击,某品牌奶糖生产企业研制出甲、乙两种新配方奶糖,已试销近三个月、已知这两种奶糖的成本价相同,售价也相同(售价不低于成本价)、为了解销售情况,营销人员进行了市场调查,并对某区域的销售数据进行了分析,发现甲、乙两种配方奶糖的日销量Q甲、Q乙(千克)与它们的售价x(元/千克)之间均具有一次函数关系,部分数据见右表.又知当售价为25元时,甲种配方奶糖的日销售利润为450元.[注:日销售利润=(销售价-成本价)×日销售量.]
(1)根据上述信息,研究人员求出Q乙=-2x+135.请你求出Q甲关于x的函数解析式,并写出定义域;
(2)求甲种配方奶糖的日销售利润W乙(元)关于x的函数解析式;
(3)根据上述信息,试分析当售价为多少元时,该区域甲、乙两种配方奶糖的日销售利润之和最大,并求出最大值.
| X | …. | 25 | 30 | …. |
| Q甲 | …. | 90 | 75 | …. |
| Q乙 | …. | 85 | 75 | … |
(2)求甲种配方奶糖的日销售利润W乙(元)关于x的函数解析式;
(3)根据上述信息,试分析当售价为多少元时,该区域甲、乙两种配方奶糖的日销售利润之和最大,并求出最大值.
 三点.
三点.
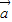 、
、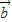 ,且
,且 .
.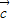 ;
; ,试说明
,试说明 ∥
∥ .
.