题目内容
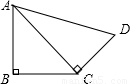
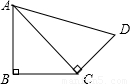
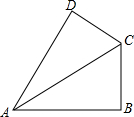如图、AB⊥CB于B，AD=24，AB=20，BC=15，CD=7，求四边形ABCD的面积．
解：∵AC=
=
=25，
故有AD2+CD2=242+72=252=AC2，
∴∠D=90°，
∴S四边形ABCD=S△ABC+S△ACD=
×20×15+×7×24=150+84=234．
分析：先运用勾股定理求出AC的长度，从而利用勾股定理的逆定理判断出△ADC是直角三角形，然后可将S四边形ABCD=S△ABC+S△ACD进行求解．
点评：本题考查勾股定理及其逆定理的知识，比较新颖，解答本题的关键是判断出△ABC是直角三角形．
==25，故有AD2+CD2=242+72=252=AC2，
∴∠D=90°，
∴S四边形ABCD=S△ABC+S△ACD=
×20×15+×7×24=150+84=234．分析：先运用勾股定理求出AC的长度，从而利用勾股定理的逆定理判断出△ADC是直角三角形，然后可将S四边形ABCD=S△ABC+S△ACD进行求解．
点评：本题考查勾股定理及其逆定理的知识，比较新颖，解答本题的关键是判断出△ABC是直角三角形．
练习册系列答案
相关题目
如图，AB⊥CB于点B，AC⊥CD于点C，AB=6，AC=10，当CD=
如图、AB⊥CB于B，AD=24，AB=20，BC=15，CD=7，求四边形ABCD的面积．
