题目内容
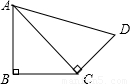
如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD= 时,△ABC∽△ACD.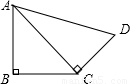
【答案】分析:根据已知,利用两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,根据相似三角形的边对应成比例求得CD的长.
解答:解:∵AB⊥CB,AC⊥CD,AB=6,AC=10,
∴∠B=∠ACD=90°,BC=8,
∵△ABC∽△ACD
∴当AB:BC=AC:CD时
∴ ,
,
解得CD= .
.
点评:此题考查了相似三角形的判定:如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似.
解答:解:∵AB⊥CB,AC⊥CD,AB=6,AC=10,
∴∠B=∠ACD=90°,BC=8,
∵△ABC∽△ACD
∴当AB:BC=AC:CD时
∴
 ,
,解得CD=
 .
.点评:此题考查了相似三角形的判定:如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD=
如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD=