Question

【题目】如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是⊙O外一点，PA切⊙O于点A，且PA=PB．

（1）求证：PB是⊙O的切线；

（2）已知PA=2，BC=2．求⊙O的半径．

Answer 1

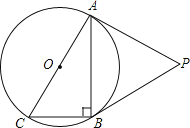
【答案】（1）证明见解析（2）圆的半径为2

【解析】(1)、连接OB，由OC=OB，PA=PB，利用等边对等角得到两对角相等，再利用弦切角等于夹弧所对的圆周角得到一对角相等，等量代换得到四个角都相等，由∠ABC为直角，得到∠OBC与∠OBA互余，等量代换得到∠OBA与∠PBA互余，即OB垂直于BP，即可确定出BP为圆的切线；(2)、设圆的半径为r，则AC=2r，在直角三角形ABC中，由AC与BC，利用勾股定理表示出AB，由（1）得到三角形PAB与三角形OCB相似，由相似得比例，将各自的值代入列出关于r的方程，求出方程的解得到r的值，即为圆的半径．

（1）证明：连接OB，∵OC=OB，AB=BP，∴∠OCB=∠OBC，∠PAB=∠PBA，

∵AP为圆O的切线，∴∠PAB=∠C，∴∠PBA=∠OBC，∵∠ABC=90°，

∴∠OBC+∠OBA=90°，∴∠PBA+∠OBA=90°，即∠PBO=90°，则BP为圆O的切线；

（2）解：设圆的半径为r，则AC=2r，在Rt△ABC中，AC=2r，BC=2，

根据勾股定理得：AB==2，∵∠PAB=∠C，∠PBA=∠OBC，

∴△PAB∽△OCB， ∴，即，∴r=2，

∴r2（r2﹣1）=12， ∴r12=4，r22=﹣3（舍）， ∴r1=2，r2=﹣2（舍）， 则圆的半径为2．