题目内容
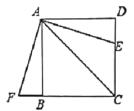
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)如图,求证:矩形![]() 是正方形;
是正方形;

(2)当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,求
时,求![]() 的度数.
的度数.
【答案】∠EFC=125°或145°.
【解析】
(1)首先作EP⊥CD于P,EQ⊥BC于Q,由∠DCA=∠BCA,得出EQ=EP,再由∠QEF+∠FEC=45°,得出∠PED+∠FEC=45°,进而得出∠QEF=∠PED,即可判定Rt△EQF≌Rt△EPD,得出EF=ED,即可得证;
(2)分类讨论:①当DE与AD的夹角为35°时,∠EFC=125°;②当DE与DC的夹角为35°时,∠EFC=145°,即可得解.
(1)作EP⊥CD于P,EQ⊥BC于Q,如图所示
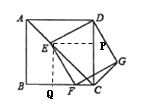
∵∠DCA=∠BCA
∴EQ=EP,
∵∠QEF+∠FEP=90°,∠PED+∠FEP=90°,
∴∠QEF=∠PED
在Rt△EQF和Rt△EPD中,
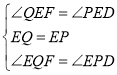
∴Rt△EQF≌Rt△EPD
∴EF=ED
∴矩形DEFG是正方形;
(2)①当DE与AD的夹角为35°时,
∠DEP=∠QEF=35°,
∴∠EFQ=90°-35°=55°,
∠EFC=180°-55°=125°;
②当DE与DC的夹角为35°时,
∠DEP=∠QEF=55°,
∴∠EFQ=90°-55°=35°,
∠EFC=180°-35°=145°;
综上所述,∠EFC=125°或145°.

练习册系列答案
相关题目