Question

【题目】如图，在矩形ABCD中，AB＝6，BC＝13，BE＝4，点F从点B出发，在折线段BA﹣AD上运动，连接EF，当EF⊥BC时停止运动，过点E作EG⊥EF，交矩形的边于点G，连接FG．设点F运动的路程为x，△EFG的面积为S．

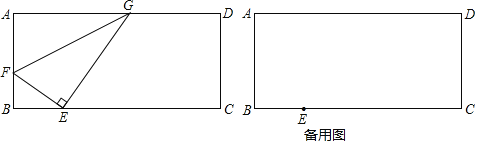
（1）当点F与点A重合时，点G恰好到达点D，此时x＝　 　，当EF⊥BC时，x＝　 　；

（2）求S关于x的函数解析式，并直接写出自变量x的取值范围；

（3）当S＝15时，求此时x的值．

Answer 1

【答案】（1）6；10；（2）S＝x2+9x+12（0＜x≤6）；S＝x2﹣21x+102（6＜x≤10）；（3）﹣6+2．

【解析】

（1）当点F与点A重合时，x＝AB＝6；当EF⊥BC时，AF＝BE＝4，x＝AB+AF＝6+4＝10；

（2）分两种情况：①当点F在AB上时，作GH⊥BC于H，则四边形ABHG是矩形，证明△EFB∽△GEH，得出，求出EH＝x，得出AG＝BH＝BE+EH＝4+x，由梯形面积公式和三角形面积公式即可得出答案；

②当点F在AD上时，作FM⊥BC于M，则FM＝AB＝6，AF＝BM，同①得△EFM∽△GEC，得出，求出GC＝15﹣x，得出DG＝CD﹣CG＝x﹣9，EC＝BC﹣BE＝9，AF＝x﹣6，DF＝AD﹣AF＝19﹣x，由梯形面积公式和三角形面积公式即可得出答案；

（3）当x2+9x+12＝15时，当x2﹣21x+102＝15时，分别解方程即可．

（1）当点F与点A重合时，x＝AB＝6；

当EF⊥BC时，AF＝BE＝4，x＝AB+AF＝6+4＝10；

故答案为：6；10；

（2）∵四边形ABCD是矩形，

∴∠B＝∠C＝∠D＝90°，CD＝AB＝6，AD＝BC＝13，

分两种情况：

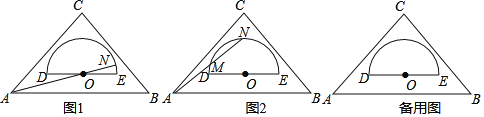
①当点F在AB上时，如图1所示：

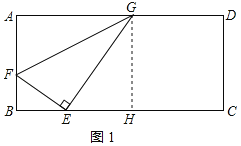
作GH⊥BC于H，

则四边形ABHG是矩形，

∴GH＝AB＝6，AG＝BH，∠GHE＝∠B＝90°，

∴∠EGH+∠GEH＝90°，

∵EG⊥EF，

∴∠FEB+∠GEH＝90°，

∴∠FEB＝∠EGH，

∴△EFB∽△GEH，

∴，即，

∴EH＝x，

∴AG＝BH＝BE+EH＝4+x，

∴△EFG的面积为S＝梯形ABEG的面积﹣△EFB的面积﹣△AGF的面积＝（4+4+x）×6﹣×4x﹣（6﹣x）（4+x）＝x2+9x+12，

即S＝x2+9x+12（0＜x≤6）；

②当点F在AD上时，如图2所示：

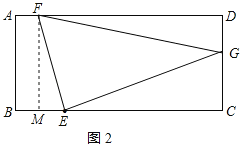
作FM⊥BC于M，则FM＝AB＝6，AF＝BM，

同①得：△EFM∽△GEC，

∴，即，

解得：GC＝15﹣x，

∴DG＝CD﹣CG＝x﹣9，

∵EC＝BC﹣BE＝9，AF＝x﹣6，DF＝AD﹣AF＝19﹣x，

∴△EFG的面积为S＝梯形CDFE的面积﹣△CEG的面积﹣△DFG的面积

＝（9+19﹣x）×6﹣×9×（15﹣x）﹣（19﹣x）（x﹣9）＝x2﹣21x+102

即S＝x2﹣21x+102（6＜x≤10）；

（3）当x2+9x+12＝15时，

解得：x＝﹣6±（负值舍去），

∴x＝﹣6+；

当x2﹣21x+102＝15时，

解得：x＝14±（不合题意舍去）；

∴当S＝15时，此时x的值为﹣6+．