题目内容
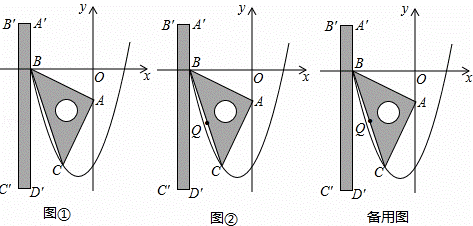
如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数y=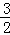 x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ=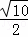 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)


解:
(1)
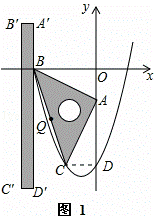
如图1,过点C作CD⊥y轴于D,此时△CDA≌△AOB,
∵△CDA≌△AOB,
∴AD=BO=2,CD=AO=1,
∴OD=OA+AD=3,
∴C(﹣1,﹣3).
将B(﹣2,0),C(﹣1,﹣3)代入抛物线y=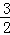 x2+bx+c,
x2+bx+c,
解得 b=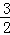 ,c=﹣3,
,c=﹣3,
∴抛物线的解析式为y=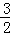 x2+
x2+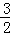 x﹣3.
x﹣3.
(2)
设lBC:y=kx+b,
∵B(﹣2,0),C(﹣1,﹣3),
∴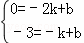 ,
,
解得 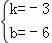 ,
,
∴lBC:y=﹣3x﹣6,
设M(xM,﹣3xM﹣6),N(xN,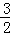 xN2+
xN2+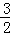 xN﹣3),
xN﹣3),
∵xM=xN(记为x),yM≥yN,
∴线段MN长度=﹣3x﹣6﹣(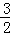 x2+
x2+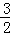 x﹣3)=﹣
x﹣3)=﹣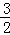 (x+
(x+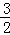 )2+
)2+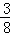 ,(﹣2≤x≤﹣1),
,(﹣2≤x≤﹣1),
∴当x=﹣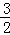 时,线段MN长度为最大值
时,线段MN长度为最大值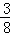 .
.
(3)
答:P在抛物线外时,BP2+CP2≥PA2;P在抛物线上时,BP+CP=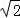 AP;P在抛物线内,BP2+CP2≥PA2.
AP;P在抛物线内,BP2+CP2≥PA2.
分析如下:
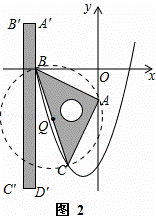
如图2,以Q点为圆心,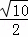 为半径作⊙Q,
为半径作⊙Q,
∵OB=2,OA=1,
∴AC=AB=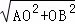 =
=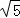 ,
,
∴BC=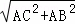 =
=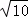 ,
,
∴BQ=CQ=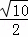 ,
,
∵∠BAC=90°,
∴点B、A、C都在⊙Q上.
①P在抛物线外,
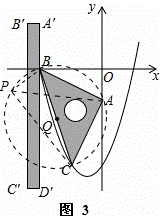
如图3,在抛物线外的弧BC上任找一点P,连接PB,PB,PA,
∵BC为直径,
∴BP2+CP2=BC2,BC≥PA,
∴BP2+CP2≥PA2.
②P在抛物线上,此时,P只能为B点或者C点,
∵AC=AB=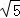 ,
,
∴AP=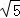 ,
,
∵BP+CP=BC=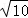 ,
,
∴BP+CP=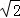 AP.
AP.
③P在抛物线内,同理①,
∵BC为直径,
∴BP2+CP2=BC2,BC≥PA,
∴BP2+CP2≥PA2.
点评: 本题考查了三角形全等、抛物线图象与性质、函数性质及圆的基础知识,是一道综合性比较强的题目.



 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
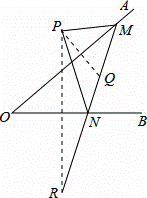
|
| A. | 4.5 | B. | 5.5 | C. | 6.5 | D. | 7 |


平行四边形的内角和为( )
|
| A. | 180° | B. | 270° | C. | 360° | D. | 640° |
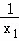 +
+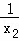 =1,求
=1,求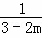 的值;
的值;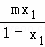 +
+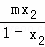 ﹣m2的最大值.
﹣m2的最大值.
 取1.73,结果精确到0.1m)
取1.73,结果精确到0.1m)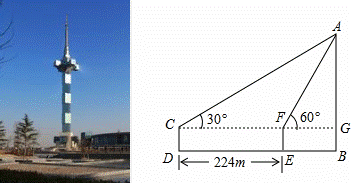
 =
= +
+ B. (
B. (