题目内容
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
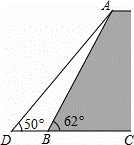
解:过A点作AE⊥CD于E.
在Rt△ABE中,∠ABE=62°.
∴AE=AB•sin62°=25×0.88=22米,
BE=AB•cos62°=25×0.47=11.75米,
在Rt△ADE中,∠ADB=50°,
∴DE= =18
=18 米,
米,
∴DB=DC﹣BE≈6.58米.
故此时应将坝底向外拓宽大约6.58米.


练习册系列答案
相关题目
二次函数y=ax2+b(b>0)与反比例函数y= 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
|
| A. |
| B. |
| C. |
| D. |
|
如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )

|
| A. | π | B. | 2π | C. |
| D. | 4π |
2的绝对值是( )
|
| A. | ±2 | B. | 2 | C. |
| D. | ﹣2 |
若方程x2+x﹣1=0的两实根为α、β,那么下列说法不正确的是( )
|
| A. | α+β=﹣1 | B. | αβ=﹣1 | C. | α2+β2=3 | D. |
|
 x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.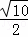 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.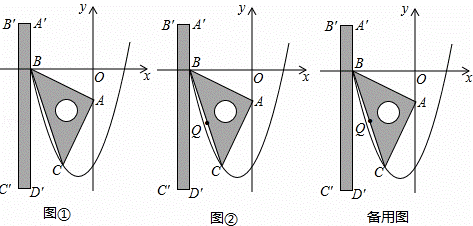







 +
+ =﹣1
=﹣1