题目内容
设m是不小于﹣1的实数，使得关于x的方程x2+2（m﹣2）x+m2﹣3m+3=0有两个不相等的实数根1，x2．
（1）若
+
=1，求
的值；
（2）求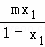
+
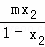﹣m2的最大值．
解：∵方程有两个不相等的实数根，
∴△=b2﹣4ac=4（m﹣2）2﹣4（m2﹣3m+3）=﹣4m+4＞0，
∴m＜1，
结合题意知：﹣1≤m＜1．
（1）∵x1+x2=﹣2（m﹣2），x1x2=m2﹣3m+3
∴+=
=
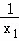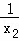=1
解得：m1=
，m2=
（不合题意，舍去）
∴
=
﹣2．
（2）
+
﹣m2
=
﹣m2
=﹣2（m﹣1）﹣m2
=﹣（m+1）2+3．
当m=﹣1时，最大值为3．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
在实数范围内有意义，则实数
的取值范围是 ( )
（B）
（D）
C． 3.8×1011 D． 3.8×1012
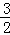x2+bx+c的图象经过B、C两点．现将一把直尺放置在直角坐标系中，使直尺的边A′D′∥y轴且经过点B，直尺沿x轴正方向平移，当A′D′与y轴重合时运动停止．
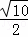时，线段PA、PB、PC之间的数量关系．请直接写出结论，并指出相应的点P与抛物线的位置关系．
二次函数y=ax2+b（b＞0）与反比例函数y=
在同一坐标系中的图象可能是（ ）
|
| A． |
| B． |
| C． |
| D． |
|
