题目内容
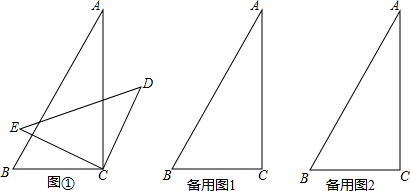
17.将一副三角板中的两根直角顶点C叠放在一起(如图①),其中∠A=30°,∠B=60°,∠D=∠E=45°.(1)若∠BCD=150°,求∠ACE的度数;
(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;
(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
分析 (1)由∠BCD=150°,∠ACB=90°,可得出∠DCA的度数,进而得出∠ACE的度数;
(2)根据(1)中的结论可提出猜想,再由∠BCD=∠ACB+∠ACD,∠ACE=∠DCE-∠ACD可得出结论;
(3)根据平行线的判定定理,画出图形即可求解.
解答 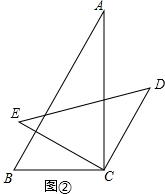 解:(1)∵∠BCA=∠ECD=90°,∠BCD=150°,
解:(1)∵∠BCA=∠ECD=90°,∠BCD=150°,
∴∠DCA=∠BCD-∠BCA=150°-90°=60°,
∴∠ACE=∠ECD-∠DCA=90°-60°=30°;
(2)∠BCD+∠ACE=180°,理由如下:
∵∠BCD=∠ACB+∠ACD=90°+∠ACD,
∠ACE=∠DCE-∠ACD=90°-∠ACD,
∴∠BCD+∠ACE=180°;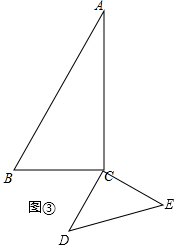
(3)当∠BCD=120°或60°时,CD∥AB.
如图②,根据同旁内角互补,两直线平行,
当∠B+∠BCD=180°时,CD∥AB,此时∠BCD=180°-∠B=180°-60°=120°;
如图③,根据内错角相等,两直线平行,
当∠B=∠BCD=60°时,CD∥AB.
点评 本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.熟练掌握定理并且能够准确识图是解题的关键.

练习册系列答案
相关题目
7.下列命题中真命题的个数是( )
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直平分且相等 |
9.根据下列表述,能确定具体位置的是( )
| A. | 奥斯卡影院2号厅3排 | B. | 汝南县汝宁大街 | ||
| C. | 东经118° | D. | 天中山北偏东60°,10km处 |
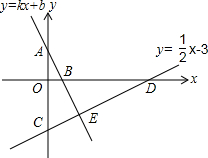 如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.
如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.