题目内容
10.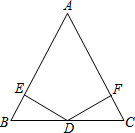 如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
分析 (1)根据DE⊥AB,DF⊥AC,AB=AC,求证∠B=∠C.再利用D是BC的中点,求证△BED≌△CFD即可得出结论.
(2)根据AB=AC,∠A=60°,得出△ABC为等边三角形.然后求出∠BDE=30°,再根据题目中给出的已知条件即可算出△ABC的周长.
解答 (1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C(等边对等角).
∵D是BC的中点,
∴BD=CD.
在△BED和△CFD中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠B=∠C}\\{BD=CD}\end{array}\right.$,
∴△BED≌△CFD(AAS).
∴DE=DF
(2)解:∵AB=AC,∠A=60°,
∴△ABC为等边三角形.
∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴BE=$\frac{1}{2}$BD,
∵BE=2,
∴BD=4,
∴BC=2BD=8,
∴△ABC的周长为24.
点评 此题主要考查学生对等边三角形的判定与性质、全等三角形的判定与性质、直角三角形的性质等知识点的理解和掌握.

练习册系列答案
相关题目
2. 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )| A. | BD=AD | B. | AB=AC | C. | ∠1=∠2 | D. | 以上答案都不对 |
19.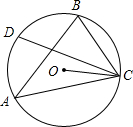 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )| A. | $\frac{β-α}{2}$ | B. | $\frac{α-β}{3}$ | C. | $\frac{β+α}{3}$ | D. | $\frac{β+α}{4}$ |
20. 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )| A. | a<0 | B. | b<c | C. | b>a | D. | c>0 |
 如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长.
如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长.
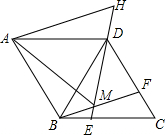 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长DE到H使DE=BM,连接AM、AH.则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;其中正确结论的个数是( )
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长DE到H使DE=BM,连接AM、AH.则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;其中正确结论的个数是( )