Question

【题目】如图，抛物线与直线y=x+3分别交于x轴和y轴上同一点，交点分别是点A和点C，且抛物线的对称轴为x=﹣2．

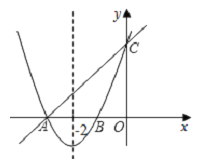
（1）求出抛物线与x轴的两个交点A、B的坐标．

（2）求出该抛物线的解析式．

Answer 1

【答案】（1）A(-3，0) B（-1，0）（2）y=x2+4x+3

【解析】

（1）由直线方程易求点A的坐标；然后根据抛物线的对称性来求点B的坐标；

（2）把点A、B、C的坐标代入抛物线解析式，利用方程组来求系数a、b、c的值．

（1）∵直线方程是y=x+3，

∴当y=0时，x=-3，

∴A（-3，0），

又∵抛物线y=ax2+bx+c与直线y=x+3交与点，且抛物线的对称轴为直线x=-2，

∴B（-1，0），

综上所述，抛物线与x轴的两个交点A、B的坐标分别是：A（-3，0）、B（-1，0）；

（2）由（1）知，A（-3，0）、B（-1，0），

∵直线方程是y=x+3，

∴当x=0时，y=3，

∴C（0，3），

依题意得，

解得．

故该抛物线的解析式是：y=x2+4x+3．