题目内容
 关于x的二次函数y=x2+2x+k-1的图象与x轴有交点,k为正整数.
关于x的二次函数y=x2+2x+k-1的图象与x轴有交点,k为正整数.(1)求k的值;
(2)当关于x的二次函数y=x2+2x+k-1与x轴的交点的横坐标均是负整数时,将关于x的二次函数y=x2+2x+k-1的图象向下平移4个单位,求平移后的图象的解析式;
(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线y=
| 1 |
| 2 |
考点:二次函数综合题
专题:
分析:(1)综合根的判别式及k的要求,求出k的取值;
(2)对k的取值进行一一验证,求出符合要求的k值,再结合抛物线平移的规律写出其平移后的解析式;
(3)求出新抛物线与x轴的交点坐标,再分别求出直线y=
x+b经过点A、B时的b的取值,进而求出其取值范围.
(2)对k的取值进行一一验证,求出符合要求的k值,再结合抛物线平移的规律写出其平移后的解析式;
(3)求出新抛物线与x轴的交点坐标,再分别求出直线y=
| 1 |
| 2 |
解答:解:(1)由题意得,△=4-4(k-1)≥0.
∴k≤2.
∵k为正整数,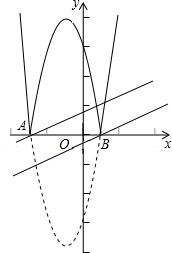
∴k=1,2;
(2)设方程x2+2x+k-1=0的两根为x1,x2,则
x1+x2=-2,x1•x2=k-1.
当k=1时,图象y=x2+2x+k-1与x轴有一个交点为(0,0),不合题意;
当k=2时,图象y=x2+2x+k-1与x轴有一个交点为(-1,0),符合题意;
综上所述,k=2符合题意.
当k=2时,二次函数为y=x2+2x+1,把它的图象向下平移4个单位得到的图象的解析式为:y=x2+2x-3;
(3)设二次函数y=x2+2x-3的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
当直线y=
x+b经过A点时,可得b=
;
当直线y=
x+b经过B点时,可得b=-
.
由图象可知,符合题意的b(b<3)的取值范围为:-
<b<
.
∴k≤2.
∵k为正整数,

∴k=1,2;
(2)设方程x2+2x+k-1=0的两根为x1,x2,则
x1+x2=-2,x1•x2=k-1.
当k=1时,图象y=x2+2x+k-1与x轴有一个交点为(0,0),不合题意;
当k=2时,图象y=x2+2x+k-1与x轴有一个交点为(-1,0),符合题意;
综上所述,k=2符合题意.
当k=2时,二次函数为y=x2+2x+1,把它的图象向下平移4个单位得到的图象的解析式为:y=x2+2x-3;
(3)设二次函数y=x2+2x-3的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
当直线y=
| 1 |
| 2 |
| 3 |
| 2 |
当直线y=
| 1 |
| 2 |
| 1 |
| 2 |
由图象可知,符合题意的b(b<3)的取值范围为:-
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题主要考查了一元二次方程根的判别式、二次函数及函数图象的平移与翻折,最后还考到了与一次函数的结合等问题.不错的题目,难度不大,综合性强.

练习册系列答案
相关题目
| 3 | 64 |
| A、4 | B、±8 | C、2 | D、±2 |
下列计算中,正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、-
|

 如图,一长方体木板,长、宽、高分别为30cm,10cm,30cm,一只蚂蚁从A点出发到B点处吃食,需要爬行的最短路程是多少?
如图,一长方体木板,长、宽、高分别为30cm,10cm,30cm,一只蚂蚁从A点出发到B点处吃食,需要爬行的最短路程是多少?