题目内容
(2011•长宁区一模)在等边三角形中,边长与高的比值是
.
2
| ||
| 3 |
2
| ||
| 3 |
分析:先根据△ABC是等边三角形,易知AB=BC=AC,∠BAC=∠B=∠C=60°,而AD是BC上的高,利用等腰三角形三线合一定理可得BD=CD=
BC,并且设△ABC的边长等于a,即BD=
a,在Rt△ABD中利用勾股定理可求AD,进而可求AB、AD的比值.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:如右图所示,
解:如右图所示,
△ABC是等边三角形,AD是边BC上的高,
∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠C=60°,
又∵AD⊥BC,
∴BD=CD=
BC,
设AB=BC=AC=a,那么BD=CD=
a,
在Rt△ABD中,AD=
=
=
a,
∴AB:AD=a:
a=
.
故答案为:
.
 解:如右图所示,
解:如右图所示,△ABC是等边三角形,AD是边BC上的高,
∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠C=60°,
又∵AD⊥BC,
∴BD=CD=
| 1 |
| 2 |
设AB=BC=AC=a,那么BD=CD=
| 1 |
| 2 |
在Rt△ABD中,AD=
| AB2-BD2 |
a2-
|
| ||
| 2 |
∴AB:AD=a:
| ||
| 2 |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查了等边三角形的性质、等腰三角形三线合一定理、勾股定理.解题的关键是求出AD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
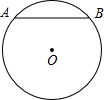 (2011•长宁区一模)已知⊙O的半径是5cm.弦AB=8cm.
(2011•长宁区一模)已知⊙O的半径是5cm.弦AB=8cm.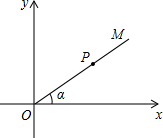 (2011•长宁区一模)如图,在直角坐标系中,∠α的顶点与坐标原点O重合,一边在x轴正半轴上,另一边是射线OM.已知cotα=
(2011•长宁区一模)如图,在直角坐标系中,∠α的顶点与坐标原点O重合,一边在x轴正半轴上,另一边是射线OM.已知cotα=