题目内容
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的一点,
上的一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .若
.若![]() 是
是![]() 的中点,则
的中点,则![]() 的长是________.
的长是________.

【答案】10.5
【解析】
根据线段中点的定义可得CG=DG,然后利用“角边角”证明△DEG和△CFG全等,根据全等三角形对应边相等可得DE=CF,EG=FG,设DE=x,表示出BF,再利用勾股定理列式求EG,然后表示出EF,再根据线段垂直平分线上的点到两端点的距离相等可得BF=EF,然后列出方程求出x的值,从而求出AD,再根据矩形的对边相等可得BC=AD.
∵矩形ABCD中,G是CD的中点,AB=12,
∴CG=DG=![]() CD=
CD=![]() AB =
AB =![]() ×12=6,
×12=6,
在△DEG和△CFG中,
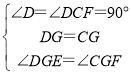 ,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=![]() ,
,
则BF=BC+CF=AD+CF=![]() ,
,
在Rt△DEG中,
EG=![]() ,
,
∴EF=2 EG=2![]() ,
,
∵FH垂直平分BE,
∴BF=EF,
∴![]() 2
2![]() ,
,
解得![]() ,
,
∴AD=AE+DE![]() ,
,
∴BC=AD=10.5.
故答案为:10.5.

练习册系列答案
相关题目