题目内容
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.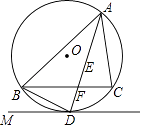
【答案】解:(Ⅰ)如图所示,连接OD, ∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴ ![]() =
= ![]() ,
,
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
∴直线DM是⊙O的切线;
(Ⅱ)如图所示,连接BE,
∵点E是△ABC的内心,
∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BAE+∠ABE=∠CBD+∠CBE,
即∠BED=∠EBD,
∴DB=DE,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴ ![]() =
= ![]() ,即DB2=DFDA,
,即DB2=DFDA,
∴DE2=DFDA.

【解析】(Ⅰ)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线; (Ⅱ)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DFDA,据此可得DE2=DFDA.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
相关题目