Question

【题目】在平面直角坐标系中，点A，B，C的坐标分别为A（a，3），B（b，6），C（m+6，1），且a，b满足

（1）请用含m的式子表示A，B两点的坐标；

（2）如图，点A在第二象限，点B在第一象限，连接A、B、C、O四点；

①若点B到y轴的距离不小于点A到y轴距离的2倍，试求m的取值范围；

②若三角形AOC的面积等于三角形ABC面积的，求实数m的值．

Answer 1

【答案】（1），；（2）；（3）

【解析】

（1）解二元一次方程组求出a，b的值，即可用含m的式子表示A，B两点的坐标；

（2）①根据点的坐标性质、结合题意列出不等式，计算即可；

②分别求出△ABC的面积和△AOC的面积，根据题意列方程，解方程得到答案．

（1，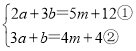

②×3-①得，7a=7m，

解得，a=m，

把a=m代入①得，b=m+4，

则A点的坐标为（m，3），B点的坐标为（m+4，6）；

（2）①∵点A在第二象限，点B在第一象限，

∴m＜0，m+4＞0，

解得，-4＜m＜0，

由题意得，m+4≥-2m，

解得，m≥-，

则-≤m＜0；

②△AOC的面积=×（1+3）×（m+6-m）-×（-m）×3-×（m+6）×1=m+9，

△ABC的面积=×（3+5）×（m+6-m）-×（m+4-m）×3-×（m+6-m-4）×5=13，

由题意得，m+9=×13，

解得，m=-．