题目内容
 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),请写出图象过点P的正比例函数解析式________.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),请写出图象过点P的正比例函数解析式________.
y= x
x
分析:过P作PE⊥MN于E,求出MN,根据垂径定理求出EM、EN,在△PME中,根据勾股定理求出PE,即可得出P的坐标,设图象过点P的正比例函数解析式是y=kx,把P的坐标代入求出即可.
解答: 解:过P作PE⊥MN于E,
解:过P作PE⊥MN于E,
∵M(0,-4),N(0,-10),
∴MN=6,
由垂径定理得:ME=NE= MN=3,
MN=3,
在Rt△PEM中,PM=5,EM=3,由勾股定理得:PE=4,
∵OE=ON-EN=10-3=7,
∴P的坐标是(-4,-7),
设图象过点P的正比例函数解析式是y=kx,
把P的坐标代入得:-7=-4k,
k= ,
,
故答案为:y= x.
x.
点评:本题考查了坐标与图形性质,垂径定理,勾股定理,用待定系数法求正比例函数的解析式等知识点,主要考查了学生的计算能力和推理能力.
 x
x分析:过P作PE⊥MN于E,求出MN,根据垂径定理求出EM、EN,在△PME中,根据勾股定理求出PE,即可得出P的坐标,设图象过点P的正比例函数解析式是y=kx,把P的坐标代入求出即可.
解答:
 解:过P作PE⊥MN于E,
解:过P作PE⊥MN于E,∵M(0,-4),N(0,-10),
∴MN=6,
由垂径定理得:ME=NE=
 MN=3,
MN=3,在Rt△PEM中,PM=5,EM=3,由勾股定理得:PE=4,
∵OE=ON-EN=10-3=7,
∴P的坐标是(-4,-7),
设图象过点P的正比例函数解析式是y=kx,
把P的坐标代入得:-7=-4k,
k=
 ,
,故答案为:y=
 x.
x.点评:本题考查了坐标与图形性质,垂径定理,勾股定理,用待定系数法求正比例函数的解析式等知识点,主要考查了学生的计算能力和推理能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,
如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,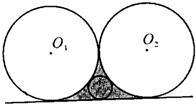 12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于
12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°. 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为