题目内容
如图所示，AD为△ABC中∠BAC的平分线，GH⊥AD于F，且交BC的延长线于E，求证：CE•BG=CH•BE．考点：相似三角形的判定与性质
专题：证明题
分析：过C作CM∥AB交GE于M，则可证得∠3=∠4，结合平行可得∠CMH=∠CHM，可证得CM=CH，又
=
，代入化为乘积可得出结论．
| CE |
| BE |
| CM |
| BG |
解答：
证明：
过C作CM∥AB交GE于M，
∵AD平分∠BAC，
∴∠1=∠2，
∵GH⊥AD，
∴∠AFG=∠AFH=90°，
∴∠3=∠4，
∵CM∥AB，
∴∠3=∠CMH，
∵∠4=∠CHM，
∴∠CMH=∠CHM，
∴CM=CH，
∵CM∥AB，
∴
=
，
∴
=
，
∴CE•BG=BE•CH．
证明：过C作CM∥AB交GE于M，
∵AD平分∠BAC，
∴∠1=∠2，
∵GH⊥AD，
∴∠AFG=∠AFH=90°，
∴∠3=∠4，
∵CM∥AB，
∴∠3=∠CMH，
∵∠4=∠CHM，
∴∠CMH=∠CHM，
∴CM=CH，
∵CM∥AB，
∴
| CE |
| BE |
| CM |
| BG |
∴
| CE |
| BE |
| CH |
| BG |
∴CE•BG=BE•CH．
点评：本题主要考查平行线分线段成比例，构造平行且证得CM=CH是解题的关键，注意角平分线及平行找角相等是常用的方法．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
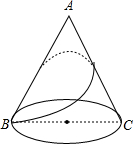有一圆锥形粮堆如图所示，其母线长为12m，底面直径长为6m，一只小猫从B处绕粮堆巡视一圈后又回到B处，则它所行走最短路程是已知⊙O上有一点A，直线l经过点A，则l与⊙O的位置关系是（ ）
| A、相切 | B、相交 |
| C、相离 | D、相交或相切 |
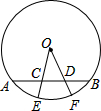如图，半径OE、OF与弦AB分别交于点C、D，
如图，有