题目内容
18.解方程:(1)(x+1)2-9=0.
(2)x2+2x-5=0.
(3)x(x-1)=2(x-1).
(4)(x-1)(x+3)=12.
分析 (1)先移项,写成(x+a)2=b的形式,然后利用数的开方解答.
(2)配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.
(3)先移项,然后利用提取公因式法进行因式分解.
(4)整理后分解因式得到x+5)(x-3)=0,推出方程x+5=0,x-3=0,求出方程的解即可.
解答 解:(1)移项得,(x+1)2=9,
开方得,x+1=±3,
解得x1=2,x2=-4.
(2)由原方程,得
x2+2x=5,
配方,得
x2+2x+1=5+1,即(x+1)2=6,
则x+1=±$\sqrt{6}$,
解得:x=-1±$\sqrt{6}$.
(3)由原方程,得
(x-2)(x-1)=0.
则x-2=0或x-1=0,
解得x1=2,x2=1.
(4)(x-1)(x+3)=12,
整理得:x2+2x-15=0,
分解因式得:(x+5)(x-3)=0,
即x+5=0,x-3=0,
解方程得:x1=-5,x2=3,
∴方程的解是x1=-5,x2=3.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列说法中,错误的是( )
| A. | 全等三角形对应角相等 | B. | 全等三角形对应边相等 | ||
| C. | 全等三角形的面积相等 | D. | 面积相等的两个三角形一定全等 |
3.为了了解大江东产业集聚区2014年数学学业考试各分数段成绩分布情况,从中抽取 1500名考生的学业考试数学成绩进行统计分析.在这个问题中,样本容量是指( )
| A. | 1500 | |
| B. | 被抽取的1500名考生的学业考试数学成绩 | |
| C. | 被抽取的1500名考生 | |
| D. | 大江东产业集聚区2014年学业考试数学成绩 |
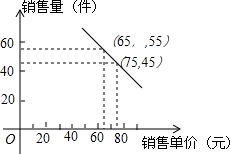 超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:
超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下: 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,C1B=CB,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2014,最少经过( )次操作.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,C1B=CB,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2014,最少经过( )次操作.