题目内容
10.如图,射线QP与等边△ABC的两边AB.AC分别交于点M.N,且BC∥QP,AM=MB=2,QP=8,将等边△ABC从如图位置(点Q与点M重合)沿射线QP以1cm/s的速度向右移动,经过t(s),以点P为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=4或5≤t≤9或t=10..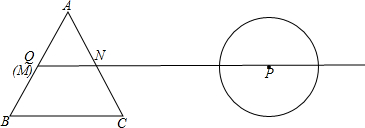
分析 求出AB=AC=BC=4cm,MN=$\frac{1}{2}$BC=2cm,∠AMN=∠ANM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;
解答  解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴AB=AC=BC=AM+MB=4,∠A=∠C=∠B=60°,
∵QN∥BC,AM=BM.
∴N为AC中点,
∴MN=$\frac{1}{2}$BC=2,∠AMN=∠ANM=∠C=∠A=60°,PN=6,
分为三种情况:
①如图1,
当⊙P切AC于D时,连接PD,
则PD=$\sqrt{3}$,∠PDN=90°,
∵∠PND=∠ANM=60°,
∴DN=1,PN=2ND=2,
∴PM=4,
∴三角形移动的距离=6-2=4,
即t=4;
②如图2,
当⊙P于BC切于C点时,连接PC,
则∠BCP=∠CPM=90°,∠PC=∠ANM=60°,CP=$\sqrt{3}$,
∴PN=1,
∴三角形移动的距离=6-1=5,
即t=5,
当⊙P于BC切于B点时,连接PB,
则∠PBC=∠BPM=90°,∠PMB=∠AMN=60°,PB=$\sqrt{3}$,
∴PM=1,
∴三角形移动的距离=4cm+2cm+1cm=9,
∴t=9,
即当5≤t≤9时,⊙P和BC边相切;
③如图3,
当⊙P切AB于E时,连接PE
则PE=$\sqrt{3}$cm,∠PEM=90°,
∵∠PME=∠AMN=60°,
∴ME=1cm,PM=2,
∴三角形移动的距离=6+2+2=10,
即t=10;
注意:由于对称性可知,当P点运动到AB右侧时也存在⊙P切AB,此时PM也是为2,即P点为N点,同理可得P点在N点时,⊙P切BC.这两点都在第二种情况运动时间内.
故答案为:t=4或5≤t≤9或t=10.
点评 本题考查了等边三角形的性质,平行线的性质,勾股定理,含30度角的直角三角形性质,切线的性质的应用,主要考查学生综合运用定理进行计算的能力,注意要进行分类讨论啊.

| A. | a5 | B. | a6 | C. | a8 | D. | a9 |