题目内容
 如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为
如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为
- A.

- B.

- C.

- D.

A
分析:先求出△AEH与△BFE相似,再根据其相似比EF:FG=3:1设出AE、BF的长及AB、BC的长,求出 的值即可.
的值即可.
解答:∵四边形EFGH是矩形ABCD的内接矩形,EF:FG=3:1,AB:BC=2:1,
∴∠HEA+∠FEB=90°,
∵∠FEB+∠EFB=90°,
∴∠HEA=∠EFB,
∵∠HAE=∠B,
∴Rt△HAE∽△EBF,
∴ =
= =
=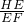 =
= ,
,
同理可得,∠GHD=∠EFB,HG=EF,
∴△GDH≌△EBF,DH=BF,DG=EB,
设AB=2x,BC=x,AE=a,BF=3a,
则AH=x-3a,AE=a,
∴tan∠AHE=tan∠BEF,
即 =
= ,解得:x=8a,
,解得:x=8a,
∴tan∠AHE= =
= =
= .
.
故选A
点评:此题比较复杂,解答此题的关键是根据题意求出相似三角形的相似比,根据各边之间的关系列出方程解答.
分析:先求出△AEH与△BFE相似,再根据其相似比EF:FG=3:1设出AE、BF的长及AB、BC的长,求出
 的值即可.
的值即可.解答:∵四边形EFGH是矩形ABCD的内接矩形,EF:FG=3:1,AB:BC=2:1,
∴∠HEA+∠FEB=90°,
∵∠FEB+∠EFB=90°,
∴∠HEA=∠EFB,
∵∠HAE=∠B,
∴Rt△HAE∽△EBF,
∴
 =
= =
=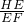 =
= ,
,同理可得,∠GHD=∠EFB,HG=EF,
∴△GDH≌△EBF,DH=BF,DG=EB,
设AB=2x,BC=x,AE=a,BF=3a,
则AH=x-3a,AE=a,
∴tan∠AHE=tan∠BEF,
即
 =
= ,解得:x=8a,
,解得:x=8a,∴tan∠AHE=
 =
= =
= .
.故选A
点评:此题比较复杂,解答此题的关键是根据题意求出相似三角形的相似比,根据各边之间的关系列出方程解答.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
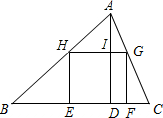 如图,四边形EFGH是△ABC内接正方形,BC=27cm,高AD=21cm,求内接正方形EFGH的面积.
如图,四边形EFGH是△ABC内接正方形,BC=27cm,高AD=21cm,求内接正方形EFGH的面积.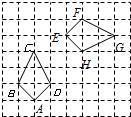 8、如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是
8、如图,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是 4、如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
4、如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )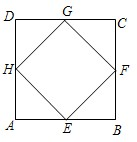 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4. 如图,四边形EFGH是△ABC内接正方形,BC=21cm,高AD=15cm.
如图,四边形EFGH是△ABC内接正方形,BC=21cm,高AD=15cm.