Question

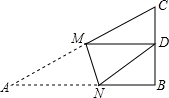
如图，五边形ABCDE中，BC=DE，AE=DC，∠C=∠E，DM⊥AB于M，试说明M是AB中点．

Answer 1

【考点】全等三角形的判定与性质；等腰三角形的性质．

【专题】证明题．

【分析】连接AD、BD．易证△ADE≌△DBC，再根据全等三角形的性质可得AD=DB，即△ABD是等腰三角形，而DM⊥AB，利用等腰三角形三线合一定理可得M是AB中点．

【解答】证明：连接AD、BD，

∵，

∴△ADE≌△DBC（SAS），

∴AD=BD，

又∵DM⊥AB，

∴M是AB的中点．

【点评】本题考查了全等三角形的判定和性质及等腰三角形三线合一定理；作出辅助线是正确解答本题的关键．