题目内容
 如图,△PQR是△ABC经过某种变换得到的图形,点A与点P、点B与点Q、点C与点R是对应点,观察它们之间的关系,设第一象限内的点M的坐标为(m,n);
如图,△PQR是△ABC经过某种变换得到的图形,点A与点P、点B与点Q、点C与点R是对应点,观察它们之间的关系,设第一象限内的点M的坐标为(m,n);(1)在这种变化下,点M的对应点为点N,在图中标出点N并写出其坐标为
(2)若连接QM、NB,请用所学知识说明QM∥NB;
(3)点E为坐标轴上一点,满足S△ABE=1.5,请写出所有符合条件的点E的坐标:
分析:(1)根据中心对称的性质标出点N的位置,然后写出坐标即可;
(2)根据对应点的坐标利用平移的性质解答;
(3)根据三角形的面积公式确定出(4,0)点,再找出关于直线AB的对称点(1,0),然后利用平移的性质找出AB的平行线与坐标轴的交点即可.
(2)根据对应点的坐标利用平移的性质解答;
(3)根据三角形的面积公式确定出(4,0)点,再找出关于直线AB的对称点(1,0),然后利用平移的性质找出AB的平行线与坐标轴的交点即可.
解答: 解:(1)点N如图所示,
解:(1)点N如图所示,
N(-m,-n);
(2)Q(-3,-1),B(3,1),M(m,n),N(-m,-n).
∵M(m,n),B(3,1),
∴点B可以看作是点M先向上平移(3-m)个单位长度,再向下平移(n-1)个单位长度得到的,
∵Q(-3,-1),N(-m,-n),
∴点N也可以看作是点Q先向上平移(3-m)个单位长度,再向下平移(n-1)个单位长度得到的,
∴线段BN可以看作是由线段MQ平移得到的,
∴QM∥BN;
(3)E1(1,0),E2(0,-2),E3(4,0),E4(0,-8).
故答案为:(-m,-n);E1(1,0),E2(0,-2),E3(4,0),E4(0,-8).
 解:(1)点N如图所示,
解:(1)点N如图所示,N(-m,-n);
(2)Q(-3,-1),B(3,1),M(m,n),N(-m,-n).
∵M(m,n),B(3,1),
∴点B可以看作是点M先向上平移(3-m)个单位长度,再向下平移(n-1)个单位长度得到的,
∵Q(-3,-1),N(-m,-n),
∴点N也可以看作是点Q先向上平移(3-m)个单位长度,再向下平移(n-1)个单位长度得到的,
∴线段BN可以看作是由线段MQ平移得到的,
∴QM∥BN;
(3)E1(1,0),E2(0,-2),E3(4,0),E4(0,-8).
故答案为:(-m,-n);E1(1,0),E2(0,-2),E3(4,0),E4(0,-8).
点评:本题考查了利用平移变换作图,中心对称的性质,三角形的面积,难点在于(3)先确定出点(4,0),再根据对称性和平移的性质求解.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
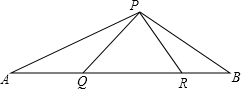 已知:如图,△PQR是等边三角形,∠APB=120°
已知:如图,△PQR是等边三角形,∠APB=120°
 如图:△PQR是等边三角形,∠APB=120°
如图:△PQR是等边三角形,∠APB=120° 已知:如图,△PQR是等边三角形,∠APB=120°
已知:如图,△PQR是等边三角形,∠APB=120°