题目内容
 如图:△PQR是等边三角形,∠APB=120°
如图:△PQR是等边三角形,∠APB=120°(1)求证:QR2=AQ•RB;
(2)若AP=2
| 7 |
| 14 |
分析:(1)利用等边三角形性质,进一步证得△AQP∽△PRB,再由三角形相似的性质解答即可.
(2)利用证得的△PAQ∽△BPR,就可得:PA:BP=AQ:PR,则可算出PR、BR的长,在等边△PQR中,PR=RQ,可求出它的高,也就是△PRB的高,由此面积也可求.
(2)利用证得的△PAQ∽△BPR,就可得:PA:BP=AQ:PR,则可算出PR、BR的长,在等边△PQR中,PR=RQ,可求出它的高,也就是△PRB的高,由此面积也可求.
解答:(1)证明:∵△PQR是等边三角形,
∴QR=PQ=PR,∠PQR=∠PRQ=∠QPR=60°,
∴∠AQP=∠PRB=120°,
∴∠A+∠APQ=60°,
又∵∠APB=120°,
∴∠A+∠B=60°,
∴∠APQ=∠B,
∴△AQP∽△PRB,
∴
=
,QR=PQ=PR,
∴QR2=AQ•RB.
(2)解:∵△PAQ∽△BPR
∴PA:BP=AQ:PR
即2
:
=2:PR
∴PR=
,
在等边△PQR中,PQ=RQ=PR=
底边RQ的高为
=
∴PQ:BR=AQ:PR,即
:BR=2:
,BR=1,
∵△PRB的高为等边△PQR的高
∴△PRB的面积为
×1×
=
.
∴QR=PQ=PR,∠PQR=∠PRQ=∠QPR=60°,
∴∠AQP=∠PRB=120°,
∴∠A+∠APQ=60°,
又∵∠APB=120°,
∴∠A+∠B=60°,
∴∠APQ=∠B,
∴△AQP∽△PRB,
∴
| PQ |
| BR |
| AQ |
| PR |
∴QR2=AQ•RB.
(2)解:∵△PAQ∽△BPR
∴PA:BP=AQ:PR
即2
| 7 |
| 14 |
∴PR=
| 2 |
在等边△PQR中,PQ=RQ=PR=
| 2 |
(
|
| ||
| 2 |
∴PQ:BR=AQ:PR,即
| 2 |
| 2 |
∵△PRB的高为等边△PQR的高
∴△PRB的面积为
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:此题主要考查等边三角形的性质,三角形相似的判定与性质以及等量代换的渗透,解题的关键是相似三角形的判定与性质的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 已知:如图,△PQR是等边三角形,∠APB=120°,
已知:如图,△PQR是等边三角形,∠APB=120°,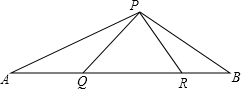 已知:如图,△PQR是等边三角形,∠APB=120°
已知:如图,△PQR是等边三角形,∠APB=120° 如图,△PQR是等边三角形,∠APB=120°,以每两个三角形为一组写出图中所有的相似三角形,并选择其中的一组加以证明.
如图,△PQR是等边三角形,∠APB=120°,以每两个三角形为一组写出图中所有的相似三角形,并选择其中的一组加以证明.