题目内容
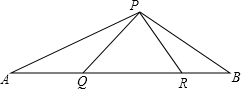 已知:如图,△PQR是等边三角形,∠APB=120°
已知:如图,△PQR是等边三角形,∠APB=120°求证:(1)△PQA∽△BRP;(2)AQ•RB=QR2.
分析:(1)由于△PQR是等边三角形,那么∠PQR=∠PRQ=60°,则∠PQA=∠BRP=120°,利用∠PQR是△PQA的外角,可得∠PQR=∠APQ+∠PAQ=60°,而∠APB=120°,利用三角形内角和定理可得∠PAQ+∠RBP=60°,于是有∠APQ=∠RBP,利用相似三角形的判定可得△PQA∽△BRP;
(2)由(1)知△PQA∽△BRP,可得比例线段
=
,而△PQR是等边三角形,可知PQ=QR=PR,于是有AQ•RB=QR2.
(2)由(1)知△PQA∽△BRP,可得比例线段
| AQ |
| PQ |
| PR |
| BR |
解答:解:(1)∵△PQR是等边三角形,
∴∠PQR=∠PRQ=60°,
∴∠PQA=∠BRP=120°,
又∵∠PQR是△PQA的外角,
∴∠PQR=∠APQ+∠PAQ=60°,
∵∠APB=120°,
∴∠PAQ+∠RBP=60°,
∴∠APQ=∠RBP,
∴△PQA∽△BRP;
(2)∵△PQA∽△BRP,
∴
=
,
又∵△PQR是等边三角形,
∴PQ=RQ=PR,
∴AQ•RB=QR2.
∴∠PQR=∠PRQ=60°,
∴∠PQA=∠BRP=120°,
又∵∠PQR是△PQA的外角,
∴∠PQR=∠APQ+∠PAQ=60°,
∵∠APB=120°,
∴∠PAQ+∠RBP=60°,
∴∠APQ=∠RBP,
∴△PQA∽△BRP;
(2)∵△PQA∽△BRP,
∴
| AQ |
| PQ |
| PR |
| BR |
又∵△PQR是等边三角形,
∴PQ=RQ=PR,
∴AQ•RB=QR2.
点评:本题利用了等边三角形的性质、相似三角形的判定和性质、三角形外角的性质、三角形的内角和定理.

练习册系列答案
相关题目
 已知:如图,△PQR是等边三角形,∠APB=120°,
已知:如图,△PQR是等边三角形,∠APB=120°, 已知:如图,△PQR是等边三角形,∠APB=120°,
已知:如图,△PQR是等边三角形,∠APB=120°,