Question

如图，PA、PB分别切⊙O于A、B，并与⊙O的另一条切线分别相交于D、C两点，已知PA=7，则△PCD的周长=

 

．

Answer 1

考点：切线长定理

专题：计算题

分析：设CD与⊙O相切于E，根据切线长定理由PA、PB分别切⊙O于A、B得到PB=PA=7cm，由于DC与⊙O相切于E，再根据切线长定理得到DA=DE，CE=CB，然后三角形周长的定义得到△PDC的周长=PD+DC+PC=PD+DE+CE+PC，然后用等线段代换后得到三角形PDC的周长等于PA+PB．

解答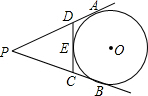：解：设CD与⊙O相切于E，
∵PA、PB分别切⊙O于A、B，
∴PB=PA=7cm，
∵DA与DE为⊙的切线，
∴DA=DE，
同理得到CE=CB，
∴△PDC的周长=PD+DC+PC=PD+DE+CE+PC
=PD+DA+CB+PC
=PA+PB
=7+7
=14（cm）．
故答案为14cm．

点评：本题考查了切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角．