题目内容
4．
如图，△ABC中，DE∥BC，∠B=72°，∠AED=40°，则∠A=（ ）| A． | 72° | B． | 70° | C． | 68° | D． | 60° |
分析 首先根据DE∥BC，可得：∠C=∠AED=40°，然后根据三角形的内角和定理，求出∠A等于多少即可．
解答 解：∵DE∥BC，
∴∠C=∠AED=40°，
又∵∠B=72°，
∴∠A=180°-72°-40°=68°．
故选：C．
点评 此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．
练习册系列答案
相关题目
如图，函数y=kx与$y=-\frac{4}{x}$的图象交于点A、B，AC⊥Oy于C，则△ABC的面积为（ ）
12．若代数式$\frac{x+1}{x-3}$有意义，则实数x的取值范围是（ ）
| A． | x≠-1 | B． | x≥一1且x≠3 | C． | x=3 | D． | x≠3 |
19．两个袋子里分别装着写有1，2，3，4的四张完全相同的卡片，从每一袋子中各随机抽取一张，则两张卡片上数字之和等于6的概率是（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{2}{16}$ | C． | $\frac{3}{16}$ | D． | $\frac{1}{2}$ |
9．下列各式能用平方差公式计算的是（ ）
| A． | （-2x-1）（1-2x） | B． | （x-3）（3-x） | C． | （x-3）（2x+3） | D． | （-x-3）（x+3） |
16．已知代数式x+2y的值是-2，则代数式3x+6y+1的值是（ ）
| A． | -3 | B． | -5 | C． | 1 | D． | 3 |
12．
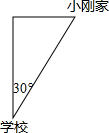如图所示，小刚家在学校的北偏东30°方向，距离学校2000米，则学校在小刚家的位置是（ ）
如图所示，小刚家在学校的北偏东30°方向，距离学校2000米，则学校在小刚家的位置是（ ）| A． | 北偏东30°，距离小刚家2000米 | B． | 南偏西60°，距离小刚家2000米 | ||
| C． | 南偏西30°，距离小刚家2000米 | D． | 北偏东60°，距离小刚家2000米 |
11．
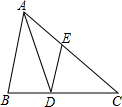如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果$\frac{CE}{AC}=\frac{3}{5}$，那么$\frac{AE}{AB}$的值为（ ）
如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果$\frac{CE}{AC}=\frac{3}{5}$，那么$\frac{AE}{AB}$的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |