Question

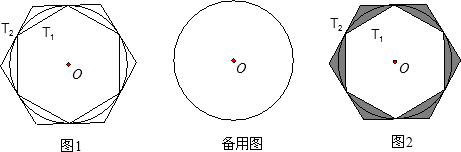
如图，，有一个圆O和两个正六边形T₁，T₂，T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切(我们称T₁，T₂分别为圆O的内接正六边形和外切正六边形)．

(1)设T₁，T₂的边长分别为a，b，圆O的半径为r，求r∶a及r∶b的值；

(2)求正六边形T₁，T₂的面积比S₁∶S₂的值．

Answer 1

答案：
解析：

(1)连接圆心O和T1的6个顶点可得6个全等的正三角形． 　　所以r∶a＝1∶1； 　　连接圆心O和T2相邻的两个顶点，得以圆O半径为高的正三角形， 　　所以r∶b＝∶2； 　　(2)T1∶T2的连长比是∶2，所以S1∶S2＝(a∶b)2＝3∶4