Question

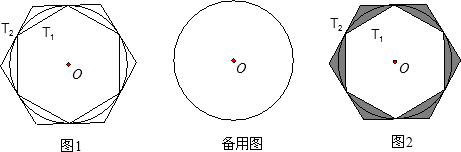
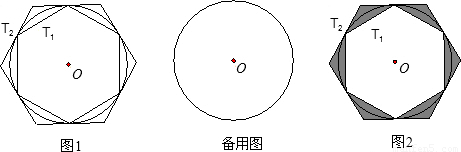
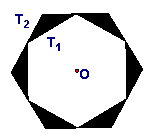
如图一，有一个圆O和两个正六边形T1，T2．T1的六个顶点都在圆周上，T2的六条边都和圆O相切（我们称T1，T2分别为圆O的内接正六边形和外切正六边形）．

（1）请你在备用图中画出圆O的内接正六边形，并简要写出作法；

（2）设圆O的半径为R，求T1，T2的边长（用含R的式子表示）；

（3）设圆O的半径为R，求图二中阴影部分的面积（用含R的式子表示）．

          

图一                   备用图                 图二

 

Answer 1

解: (1) 如图     

  作法：①在⊙O中做圆心角∠AOB＝60°；

        ②在⊙O上依次截取与弧AB相等的弧，得到圆的6个等分点A、B、C、D、E、F；

        ③顺次连接各点，六边形ABCDEF即为所求正六边形.

     

(2) ∵由（1）知△AOB为等边三角形，∴T1的半径为R;  

连接OG，可知Rt△OGB≌Rt△OGA

         ∴∠OGB＝30°∴BG＝

设BG为x，由勾股定理有：

解得：

外切正六边形的边长为

（3）由图知：

阴影部分的面积＝外切正六边形的面积－内接正六边形的面积

∵内接正六边形的面积为S△AOB的六倍 ，

 ∴内接正六边形的面积为：   

∵外切正六边形的面积为S△OGH的六倍 ，

 ∴外切正六边形的面积为：