题目内容
14.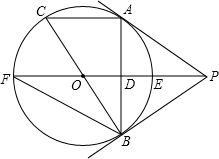 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,点F,过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交于点C,连接AC,BF.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,点F,过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交于点C,连接AC,BF.(1)求证:PB与⊙O相切;
(2)若AC=12,tan∠F=$\frac{1}{2}$,求cos∠ACB的值.
分析 (1)连接OA,由OP垂直于AB,利用垂径定理得到D为AB的中点,即OP垂直平分AB,可得出AP=BP,再由OA=OB,OP=OP,利用SSS得出三角形AOP与三角形BOP全等,由PA为圆的切线,得到OA垂直于AP,利用全等三角形的对应角相等及垂直的定义得到OB垂直于BP,即PB为圆O的切线;
(2)连接BE,构建直角△BEF.在该直角三角形中利用锐角三角函数的定义、勾股定理可设BE=x,BF=2x,进而可得EF=$\sqrt{5}$x;然后由面积法求得BD=$\frac{2\sqrt{5}}{5}$x,所以根据垂径定理求得AB的长度,在Rt△ABC中,根据勾股定理易求BC的长;最后由余弦三角函数的定义求解.
解答 (1)证明:连接OA,
∵PA与圆O相切,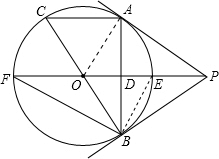
∴PA⊥OA,即∠OAP=90°,
∵OP⊥AB,
∴D为AB中点,即OP垂直平分AB,
∴PA=PB,
∵在△OAP和△OBP中,
$\left\{\begin{array}{l}{AP=BP}\\{OP=OP}\\{OA=OB}\end{array}\right.$,
∴△OAP≌△OBP(SSS),
∴∠OAP=∠OBP=90°,
∴BP⊥OB,
则直线PB为圆O的切线;
(2)解:连接BE,则∠FBE=90°.
∵tan∠F=$\frac{1}{2}$,
∴$\frac{BE}{BF}$=$\frac{1}{2}$,
∴可设BE=x,BF=2x,
则由勾股定理,得
EF=$\sqrt{B{F}^{2}+B{E}^{2}}$=$\sqrt{5}$x,
∵$\frac{1}{2}$BE•BF=$\frac{1}{2}$EF•BD,
∴BD=$\frac{2\sqrt{5}}{5}$x.
又∵AB⊥EF,
∴AB=2BD=$\frac{4\sqrt{5}}{5}$x,
∴Rt△ABC中,BC=$\sqrt{5}$x,
AC2+AB2=BC2,
∴122+( $\frac{4\sqrt{5}}{5}$x)2=( $\sqrt{5}$x)2,
解得:x=4 $\sqrt{5}$,
∴BC=4 $\sqrt{5}$×$\sqrt{5}$=20,
∴cos∠ACB=$\frac{AC}{BC}$=$\frac{12}{20}$=$\frac{3}{5}$.
点评 此题考查了切线的判定与性质,相似及全等三角形的判定与性质以及锐角三角函数关系等知识,熟练掌握切线的判定与性质是解本题的关键.

| A. | k<$\frac{1}{2}$且k≠0 | B. | k≤$\frac{1}{2}$且k≠0 | C. | k≥-$\frac{1}{2}$且k≠0 | D. | k>-$\frac{1}{2}$且k≠0 |
 如图,AD∥BE,∠GBE的平分线BF的反向延长线交AD的反向延长线于M点,若∠BAD=70°,则∠M的度数为( )
如图,AD∥BE,∠GBE的平分线BF的反向延长线交AD的反向延长线于M点,若∠BAD=70°,则∠M的度数为( )| A. | 20° | B. | 35° | C. | 45° | D. | 70° |
 如图,正方体被一个平面截去顶点为A的一个角,所得几何体的左视图是( )
如图,正方体被一个平面截去顶点为A的一个角,所得几何体的左视图是( )



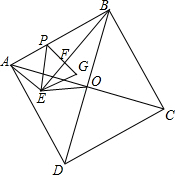 如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$.
如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$.