题目内容
已知：如图1，Rt△ABC中，∠ACB=90°，CG⊥AB，垂足为G，AD平分∠
CAB交CG于E，过E作EF∥AB，交BC于F，
=n．
（1）求证：
=
；
（2）若n=
，求
的值；
（3）当DF=1，BF=2时，求AB的值．
CAB交CG于E，过E作EF∥AB，交BC于F，| AC |
| AB |
（1）求证：
| CD |
| BD |
| AC |
| AB |
（2）若n=
| 3 |
| 5 |
| DF |
| FB |
（3）当DF=1，BF=2时，求AB的值．
分析：（1）由角平分线的性质、直角三角形的性质以及等腰三角形的判定与性质推知CE=CD；然后由相似三角形△ACE∽△ABD的对应边成比例来证得结论；
（2）设AC=3k，AB=5k．由勾股定理、∠CAG（∠CAB）的余弦三角函数的定义求得CG、CD的值；然后根据“平行线分线段成比例”、等量代换推知
=
=
，利用线段间的和差关系求得DF=k，问题到这里就迎刃可解了；
（3）由（2）知，CD=BF=1.5k，则根据已知条件“DF=1，BF=2”证得BC=5．
根据角平分线定理、余弦三角函数的定义求得
=
=
=
；然后在直角三角形ABC中根据勾股定理即可求得AB的值．
（2）设AC=3k，AB=5k．由勾股定理、∠CAG（∠CAB）的余弦三角函数的定义求得CG、CD的值；然后根据“平行线分线段成比例”、等量代换推知
| CE |
| CG |
| CF |
| BC |
| CD |
| BC |
（3）由（2）知，CD=BF=1.5k，则根据已知条件“DF=1，BF=2”证得BC=5．
根据角平分线定理、余弦三角函数的定义求得
| AC |
| AB |
| GE |
| CE |
| BF |
| BF+DF |
| 2 |
| 3 |
解答：
（1）证明：在Rt△ADC中，
∠CDA=90°-∠1（直角三角形的两锐角互余）；
同理在Rt△AEG中，
∠AEG=90°-∠2．
又∵AD平分∠CAB（已知），
∴∠1=∠2（角平分线定义），
∴∠AED=∠CDE（等量代换），
又∵∠CED=∠AED（对顶角相等），
∴∠CED=∠CDE，
∴CE=CD（等角对等边）；
在△ACE和△ABD中，
∠1=∠2，∠AEC=∠ECD+∠CDE=∠ADB，
∴△ACE∽△ABD，
∴
=
，
∴
=
；
（2）在Rt△ABC中，
=cos∠CAB=
，
故设AC=3k，AB=5k，则由勾股定理知BC=4k；
∵由（1）知
=
，
∴CD=1.5k，BD=2.5k；
在Rt△ACG中，cos∠CAG=
=cos∠CAB=
，
∴AG=
k，
∴CG=
k（勾股定理）；
又∵EF∥AB，
∴
=
（平行线分线段成比例），
∵由（1）知，CD=CE，
∴
=
，即
=
=
，
∴CF=
k，
∴DF=CF-CD=k，FB=BD-DF=1.5k，
∴
=
=
；
（3）由（2）知，CD=BF，则BC=5．
∵AD平分∠CAB，
∴
=
（角平分线定理），
又∵
=
=cos∠CAB，
∴
=
；
∵EF∥AB，
∴
=
（平行线截线段成比例），
∴
=
（比例的性质），即
=
=
=
，
∴
=
；
∵AC2+BC2=AB2，
∴AB=3
．
（1）证明：在Rt△ADC中，∠CDA=90°-∠1（直角三角形的两锐角互余）；
同理在Rt△AEG中，
∠AEG=90°-∠2．
又∵AD平分∠CAB（已知），
∴∠1=∠2（角平分线定义），
∴∠AED=∠CDE（等量代换），
又∵∠CED=∠AED（对顶角相等），
∴∠CED=∠CDE，
∴CE=CD（等角对等边）；
在△ACE和△ABD中，
∠1=∠2，∠AEC=∠ECD+∠CDE=∠ADB，
∴△ACE∽△ABD，
∴
| CE |
| BD |
| AC |
| AB |
∴
| CD |
| BD |
| AC |
| AB |
（2）在Rt△ABC中，
| AC |
| AB |
| 3 |
| 5 |
故设AC=3k，AB=5k，则由勾股定理知BC=4k；
∵由（1）知
| CD |
| BD |
| AC |
| AB |
∴CD=1.5k，BD=2.5k；
在Rt△ACG中，cos∠CAG=
| AG |
| AC |
| 3 |
| 5 |
∴AG=
| 9 |
| 5 |
∴CG=
| 12 |
| 5 |
又∵EF∥AB，
∴
| CE |
| CG |
| CF |
| BC |
∵由（1）知，CD=CE，
∴
| CF |
| BC |
| CD |
| CG |
| CF |
| 4k |
| 1.5k | ||
|
| 5 |
| 8 |
∴CF=
| 5 |
| 2 |
∴DF=CF-CD=k，FB=BD-DF=1.5k，
∴
| DF |
| FB |
| k |
| 1.5k |
| 2 |
| 3 |
（3）由（2）知，CD=BF，则BC=5．
∵AD平分∠CAB，
∴
| AG |
| AC |
| GE |
| CE |
又∵
| AG |
| AC |
| AC |
| AB |
∴
| AC |
| AB |
| GE |
| CE |
∵EF∥AB，
∴
| CF |
| BC |
| CE |
| CG |
∴
| GE |
| CE |
| BF |
| CF |
| GE |
| CE |
| BF |
| BF+DF |
| 2 |
| 1+2 |
| 2 |
| 3 |
∴
| AC |
| AB |
| 2 |
| 3 |
∵AC2+BC2=AB2，
∴AB=3
| 5 |
点评：本题考查了相似综合题：相似三角形的判定与性质、平行线分线段成比例、勾股定理、余弦三角函数的定义以及角平分线的定义．
练习册系列答案
相关题目
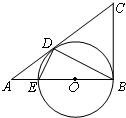53、已知：如图，在Rt△ABC中，∠ABC=90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D、
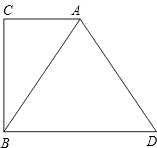已知：如图，在Rt△ABC中，∠C=90°，过点B作BD∥AC，且BD=2AC，连接AD．试判断△ABD的形状，并说明理由．
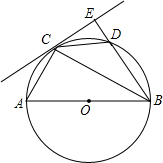已知：如图，以Rt△ABC的斜边AB为直径作⊙O，D是⊙O上的点，且有AC=CD．过点C作⊙O的切线，与BD的延长线交于点E，连接CD．
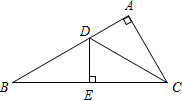已知：如图，在Rt△ABC中，∠A=90°，CD平分∠ACB交边AB于点D，DE⊥BC垂足为E，AD=
（2012•渝北区一模）已知：如图，在Rt△ABC中，∠C=90°，∠ABC=45°，D是BC上的点，BD=10．∠ADC=60°．求AC（