题目内容
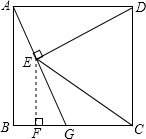
在正方形ABCD中,G是BC上一点,DE⊥AG于点E,连接EC,若AG=
BG,求
的值.
| 5 |
| GC |
| EC |
考点:平行四边形的性质,正方形的性质
专题:
分析:根据同角的余角相等求出∠BAG=∠ADE,然后利用两组角对应相等,两三角形相似求出△ABG和△DAE相似,设BG=x,AG=
x,利用勾股定理列式求出AB,再根据相似三角形对应边成比例求出AE,再求出EG,过点E作EF⊥BC于F,利用相似三角形对应边成比例求出EF、FG,然后求出CF,利用勾股定理列式表示出EC,然后求出比值即可.
| 5 |
解答:解:∵DE⊥AG,
∴∠DAE+∠ADE=90°,
∵∠BAG+∠DAE=90°,
∴∠BAG=∠ADE,
又∵∠B=∠AED=90°,
∴△ABG∽△DAE,
设BG=x,AG=
x,
由勾股定理得,AD=AB=
=2x,
则
=
,
即
=
,
解得AE=
x,
所以,EG=
x-
x=
x,
过点E作EF⊥BC于F,则△ABG∽△EFG,
∴
=
=
,
即
=
=
=
,
解得EF=
x,FG=
x,
所以,GC=2x-x=x,
CF=x+
x=
x,
由勾股定理得,EC=
=
=2x,
所以,
=
=
.
∴∠DAE+∠ADE=90°,
∵∠BAG+∠DAE=90°,
∴∠BAG=∠ADE,
又∵∠B=∠AED=90°,
∴△ABG∽△DAE,
设BG=x,AG=
| 5 |
由勾股定理得,AD=AB=
(
|
则
| BG |
| AE |
| AG |
| AD |

即
| x |
| AE |
| ||
| 2x |
解得AE=
2
| ||
| 5 |
所以,EG=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
过点E作EF⊥BC于F,则△ABG∽△EFG,
∴
| EF |
| AB |
| FG |
| BG |
| EG |
| AG |
即
| EF |
| 2x |
| FG |
| x |
| ||||
|
| 3 |
| 5 |
解得EF=
| 6 |
| 5 |
| 3 |
| 5 |
所以,GC=2x-x=x,
CF=x+
| 3 |
| 5 |
| 8 |
| 5 |
由勾股定理得,EC=
| EF2+CF2 |
(
|
所以,
| GC |
| EC |
| x |
| 2x |
| 1 |
| 2 |
点评:本题考查了正方形的性质,相似三角形的判定与性质,勾股定理,熟记性质并作辅助线构造出相似三角形是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.
如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.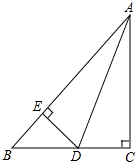 已知,如图,AD平分∠BAC,∠C=90°,DE⊥AB,那么:
已知,如图,AD平分∠BAC,∠C=90°,DE⊥AB,那么: