题目内容
【题目】如图,在四边形ABCD中,AD∥BC, ![]() ,点E是BC的中点,连接AE、BD.若EA⊥AB,BC=26,DC=12,求△ABD的面积.
,点E是BC的中点,连接AE、BD.若EA⊥AB,BC=26,DC=12,求△ABD的面积.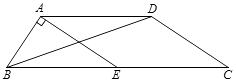
【答案】解:连接DE,
∵点E是BC的中点,BC=26,
∴BE=EC= ![]() BC=13,
BC=13,
∵AD= ![]() BC,
BC,
∴AD=BE=CE=13.
∵AD∥BE,
∴四边形ABED与四边形AECD都是平行四边形,
∴AE=DC=12,S△ABD= ![]() SABED .
SABED .
在△ABE中,
∵∠BAE=90°,
∴AB= ![]() ,
,
∴S△ABD= ![]() SABED=
SABED= ![]() ×5×12=30.
×5×12=30.
【解析】连接DE,根据点E是BC的中点,AD= ![]() BC,可得出四边形ABED与四边形AECD都是平行四边形,故可得出AE=DC=12,S△ABD=
BC,可得出四边形ABED与四边形AECD都是平行四边形,故可得出AE=DC=12,S△ABD= ![]() SABED , 根据勾股定理求出AB的长,进而可得出结论。
SABED , 根据勾股定理求出AB的长,进而可得出结论。

练习册系列答案
相关题目