题目内容
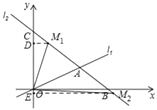
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y=![]() x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.
x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.
(1)求△OAC的面积;
(2)如点M在直线l2上,且使得△OAM的面积是△OAC面积的![]() ,求点M的坐标.
,求点M的坐标.

【答案】(1)S△OAC=12;
(2)点M的坐标为(![]() ,6﹣
,6﹣![]() )或(
)或(![]() ,6﹣
,6﹣![]() ).
).
【解析】试题分析: (1)先根据直线解析式,求得C(0,6),再根据方程组的解,得出A(4,2),进而得到△OAC的面积;
(2)分两种情况进行讨论:①点M1在射线AC上,②点M2在射线AB上,分别根据点M的横坐标,求得其纵坐标即可.
试题解析:
解:(1)在y=﹣x+6中,令x=0,解得y=6,
∴C(0,6),即CO=6,
解方程组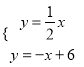 ,可得
,可得![]() ,
,
∴A(4,2),
∴S△OAC=![]() ×6×4=12;
×6×4=12;
(2)分两种情况:
①如图所示,当点M1在射线AC上时,过M1作M1D⊥CO于D,则△CDM1是等腰直角三角形,
∵A(4,2),C(0,6),
∴AC=![]() =4
=4![]() ,
,
∵△OAM的面积是△OAC面积的![]() ,
,
∴AM1=![]() AC=3
AC=3![]() ,
,
∴CM1=![]() ,
,
∴DM1=![]() ,即点M1的横坐标为
,即点M1的横坐标为![]() ,
,
在直线y=﹣x+6中,当x=![]() 时,y=6﹣
时,y=6﹣![]() ,
,
∴M1(![]() ,6﹣
,6﹣![]() );
);
②如图所示,当点M2在射线AB上时,过M2作M2E⊥CO于E,则△CEM2是等腰直角三角形,
由题可得,AM2=AM1=3![]() ,
,
∴CM2=7![]() ,
,
∴EM2=![]() ,即点M2的横坐标为
,即点M2的横坐标为![]() ,
,
在直线y=﹣x+6中,当x=![]() 时,y=6﹣
时,y=6﹣![]() ,
,
∴M2(![]() ,6﹣
,6﹣![]() ).
).
综上所述,点M的坐标为(![]() ,6﹣
,6﹣![]() )或(
)或(![]() ,6﹣
,6﹣![]() ).
).

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目