Question

【题目】已知：是等腰直角三角形，动点在斜边所在的直线上，以为直角边作等腰直角三角形，其中，探究并解决下列问题：

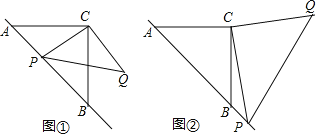
（1）如图①，若点在线段上，且．为中点，

①线段　 　；

②猜想：连接，则与的位置关系为　 　；，，三者之间的数量关系为　 　；

（2）如图②，若点在的延长线上，在（1）中所猜想的结论是否仍然成立，请你利用图②给出证明过程．

Answer 1

【答案】（1）①1；②；（2）结论仍然成立，理由见解析

【解析】

（1）①根据等腰直角三角形的性质可得，再根据中点的性质即可求出PB的长度；②连接，通过证明，可得 从而得到，即，得证为直角三角形，再根据勾股定理可得 ；

（2）过点作，垂足为．连接，根据等腰直角三角形的性质可得 即可证明 ，可得

从而可得，即 ，故为直角三角形，再根据勾股定理即可得证.．

解：（1）①，，为中点，

，，

故答案为：1

②连接，

和均为等腰直角三角形，

，即，

为直角三角形．

故答案为：；

（2）结论仍然成立，

理由如下：如图②：过点作，垂足为．连接，

和均为等腰直角三角形，

，即，

为直角三角形．

.