Question

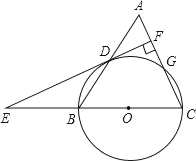
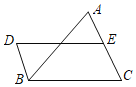
【题目】已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，PD＝2，下列结论：①EB⊥ED；②∠AEB＝135°；③S正方形ABCD＝5+2；④PB＝2；其中正确结论的序号是（　　）

A.①③④B.②③④C.①②④D.①②③

Answer 1

【答案】D

【解析】

先证明△APD≌△AEB得出BE＝PD，∠APD＝∠AEB，由等腰直角三角形的性质得出∠APE＝∠AEP＝45，得出∠APD＝∠AEB＝135，②正确；得出∠PEB＝∠AEB﹣∠AEP＝90，EB⊥ED，①正确；作BF⊥AE交AE延长线于点F，证出EF＝BF＝，得出AF＝AE+EF＝1+，由勾股定理得出AB＝＝，得出S正方形ABCD＝AB2＝5+2，③正确；EP＝AE＝，由勾股定理得出BP＝＝，④错误；即可得出结论．

解：∵∠EAB+∠BAP＝90，∠PAD+∠BAP＝90，

∴∠EAB＝∠PAD，

在△APD和△AEB中，，

∴△APD≌△AEB（SAS），

∴BE＝PD，∠APD＝∠AEB，

∵AE＝AP，∠EAP＝90，

∴∠APE＝∠AEP＝45，

∴∠APD＝135，

∴∠AEB＝135，②正确；

∴∠PEB＝∠AEB﹣∠AEP＝135﹣45＝90，

∴EB⊥ED，①正确；

作BF⊥AE交AE延长线于点F，如图所示：

∵∠AEB＝135，

∴∠EFB＝45，

∴EF＝BF，

∵BE＝PD＝2，

∴EF＝BF＝，

∴AF＝AE+EF＝1+，

AB＝＝＝，

∴S正方形ABCD＝AB2＝（）2＝5+2，③正确；

EP＝AE＝，

BP＝＝＝，④错误；

故选：D．