题目内容
9.四边形ABCD与四边形A′B′C′D′位似,O为位似中心,若OA:OA′=1:3,则S四边形ABCD:S四边形A?B?C?D?=( )| A. | 1:9 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
分析 四边形ABCD与四边形A′B′C′D′位似,四边形ABCD∽四边形A′B′C′D′,可知AD∥A′D′,△OAD∽△OA′D′,求出相似比从而求得S四边形ABCD:S四边形A?B?C?D?的值.
解答  解:∵四边形ABCD与四边形A′B′C′D′位似,
解:∵四边形ABCD与四边形A′B′C′D′位似,
∴四边形ABCD∽四边形A′B′C′D′,
∴AD∥A′D′,
∴△OAD∽△OA′D′,
∴OA:O′A′=AD:A′D′=1:3,
∴S四边形ABCD:S四边形A?B?C?D?=1:9.
故选:A.
点评 本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
17.若(a+b)2加上一个单项式后等于(a-b)2,则这个单项式为( )
| A. | 2ab | B. | -2ab | C. | 4ab | D. | -4ab |
1.有理数m、n互为相反数,x、y互为倒数,z的绝对值等于7,则m+n+5xy+z的值为( )
| A. | 12或-12 | B. | 2或-2 | C. | -12或2 | D. | 12或-2 |
18.下列各式中正确的是( )
| A. | ${({\frac{{2{x^2}}}{2y}})^3}=\frac{{2{x^6}}}{{2{y^3}}}$ | B. | ${({\frac{2a}{a+b}})^2}=\frac{{4{a^2}}}{{{a^2}+{b^2}}}$ | ||
| C. | ${({\frac{m+n}{m-n}})^3}=\frac{{{{(m+n)}^3}}}{{{{(m-n)}^3}}}$ | D. | ${({\frac{x-y}{x+y}})^2}=\frac{{{x^2}-{y^2}}}{{{x^2}+{y^2}}}$ |
19.如果两个相似三角形的相似比是1:2,那么这两个相似三角形的周长比是( )
| A. | 2:1 | B. | $1:\sqrt{2}$ | C. | 1:4 | D. | 1:2 |
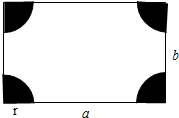 如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.