Question

如图，AB是⊙O的直径，AC和BD是它的两条切线，CO平分∠ACD．

（1）求证：CD是⊙O的切线；

（2）若AC=2，BC=3，求AB的长．

Answer 1

考点：

切线的判定与性质；勾股定理。

专题：

数形结合。

分析：

（1）过O点作OE⊥CD于点E，通过角平分线的性质得出OE=OA即可证得结论．

（2）过点D作DF⊥BC于点F，根据切线的性质可得出DC的长度，继而在RT△DFC中利用勾股定理可得出DF的长，继而可得出AB的长度．

解答：

（1）证明：过O点作OE⊥CD，垂足为E，

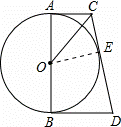
∵AC是切线，

∴OA⊥AC，

∵CO平分∠ACD，OE⊥CD，

∴OA=OE，

∴CD是⊙O的切线．

（2）解：过C点作CF⊥BD，垂足为E，

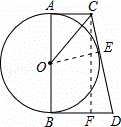
∵AC，CD，BD都是切线，

∴AC=CE=2，BD=DE=3，

∴CD=CE+DE=5，

∵∠CAB=∠ABD=∠CFB=90°，

∴四边形ABFC是矩形，

∴BF=AC=2，DF=BD﹣BF=1，

在Rt△CDF中，CF²=CD²﹣DF²=5²﹣1²=24，

∴AB=CF=2．

点评：

此题考查了切线的性质、角平分线的性质及勾股定理的知识，证明第一问关键是掌握切线的判定定理，解答第二问关键是熟练切线的性质，难度一般．