题目内容
是否存在m值，使方程（|m|-2）x2+（m+2）x+（m+1）y=m+5是关于x，y的二元一次方程？若存在，求出m的值；若不存在，请说明理由．
考点：二元一次方程的定义
专题：
分析：利用二元一次方程的定义得出其系数的关系进而求出即可．
解答：解：∵方程（|m|-2）x2+（m+2）x+（m+1）y=m+5是关于x，y的二元一次方程，
∴|m|-2=0，m+2≠0，m+1≠0，
解得：m=2．
故当m=2时，方程（|m|-2）x2+（m+2）x+（m+1）y=m+5是关于x，y的二元一次方程．
∴|m|-2=0，m+2≠0，m+1≠0，
解得：m=2．
故当m=2时，方程（|m|-2）x2+（m+2）x+（m+1）y=m+5是关于x，y的二元一次方程．
点评：此题主要考查了二元一次方程的定义，正确把握定义是解题关键．
练习册系列答案
相关题目
代数式-2x，5，3x-y，x2y，
中，单项式的个数有（ ）
| x+y |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果|x-3|+（y+2）2=0，那么x-y的值为（ ）
| A、1 | B、-1 | C、0 | D、5 |
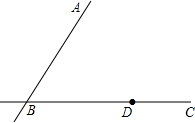已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点，求作：点E，使直线DE∥AB，且点E到B、D两点的距离相等．