��Ŀ����
ѧУ�ٰ�һ��С�������Ȼ����Ʒ�Ͻ�ʱ��Ϊ3��1����30�գ���ί���ͬѧ�ǽ�������Ʒ��ʱ��˳��ÿ5�����һ�飬��ÿһ�����Ʒ��������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ����֪�����Ҹ����εĸ߶ȱ�Ϊ2��3��4��6��4��1��������ļ�����12��
����ش�
��1�����λ������ ������Ʒ������������Ʒ�������������� ������
��2�������ȣ�������͵�����ֱ���10����2����Ʒ����ô����Ϊ���������ĸ�����ʽϸߣ�Ϊʲô��
��3��С�������Ƚ�������ί�������4�����������ƷA��B��C��D��ѡ����������ȫУչʾ��������״ͼ���б�������պ�չʾ��ƷB��D�ĸ��ʣ�
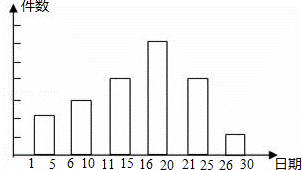
�⣺��1��������ɵó������λ�������У�12�� =12��
=12�� =60��������
=60��������
������Ʒ������������12��
�ʴ�Ϊ��60��12��
��2���ߵ���������Ʒ��60�� =18��������
=18��������
����������Ʒ��60�� =3��������
=3��������
�������Ļ���Ϊ�� =
= ��������Ļ���Ϊ��
��������Ļ���Ϊ�� ��
��
�� ��
�� ��
��
�������Ļ��ʽϸߣ�
��3������״ͼ���£�
 ��
��
����״ͼ��֪�����еȿ��ܵĽ��Ϊ12�֣����иպ��ǣ�B��D������2�֣�
���Ըպ�չʾ��ƷB��D�ĸ���Ϊ��P= =
= ��
��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д���1��2��3��4����ȡ������ͬ��������˻�����4�ĸ����ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|




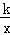 ͼ���ϵ����㣬��x1��x2=��2��x1•x2=3��y1��y2=��
ͼ���ϵ����㣬��x1��x2=��2��x1•x2=3��y1��y2=��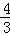 ������3��x����1ʱ����y��ȡֵ��Χ��
������3��x����1ʱ����y��ȡֵ��Χ��
 ��2��0+��
��2��0+�� ����1+4cos30�㩁|
����1+4cos30�㩁| |
|
 ����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڣ��ɵõ���P2����ʱAP2=1+
����λ�âٵ��������Ƶ�P1˳ʱ����ת��λ�âڣ��ɵõ���P2����ʱAP2=1+ ���������˹��ɼ�����ת��ֱ���õ���P2014Ϊֹ����AP2014=������
���������˹��ɼ�����ת��ֱ���õ���P2014Ϊֹ����AP2014=������
 ��
�� ��С�����ҡ��������ڵ���ȫ����
��С�����ҡ��������ڵ���ȫ���� (B)
(B)  (C)
(C)  (D)
(D) 