Question

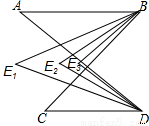
如图，已知AB∥CD，∠A=α，∠C=β，∠ABC和∠CDA的平分线交于E1，∠E1BC和∠E1DA的平分线交于E2，∠E2BC和∠E2DA的平分线交于E3，按如此方式继续下去…，用α，β的代数式表示∠BEnD的度数为　 　．

 

 

Answer 1

（α+β）

 

【解析】

根据平行线的性质得∠ABC=β，∠ADC=α，再根据角平分线的定义得∠ABE1=β，∠ADE1=α，然后利用三角形内角和定理得到∠BE1D+∠ADE1=∠A+∠ABE1，即∠BE1D+α=α+β，则∠BE1D=（α+β），同理得∠BE2D=（α+β），∠BE3D=（α+β），再利用前面的结论可得到∠BEnD=（α+β）．

【解析】
∵AB∥CD，∠A=α，∠C=β，

∴∠ABC=β，∠ADC=α，

∵∠ABC和∠CDA的平分线交于E1，

∴∠ABE1=β，∠ADE1=α

∵∠BE1D+∠ADE1=∠A+∠ABE1，即∠BE1D+α=α+β，

∴∠BE1D=（α+β），

∵∠E1BC和∠E1DA的平分线交于E2，

∴∠ABE2=β，∠ADE2=α，

∵∠BE2D+∠ADE2=∠A+∠ABE2，即∠BE1D+α=α+β，

∴∠BE2D=（α+β），

同理得∠BE3D=（α+β），

∴∠BEnD=（α+β）．

故答案为（α+β）．