题目内容
1.用适当的方法解下列方程(1)$\left\{\begin{array}{l}{2x-3y=6}\\{x=4+2y}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+3y=0}\\{3x+y=10}\end{array}\right.$
(3)$\left\{\begin{array}{l}{4x-3y=5}\\{2x-y=2}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+2y=22}\end{array}\right.$.
分析 (1)先把②代入①求出y的值,再把y的值代入②求出x的值即可;
(2)先用加减消元法求出y的值,再用代入消元法求出x的值即可;
(3)先用加减消元法求出y的值,再用代入消元法求出x的值即可;
(4)先把方程组中的方程化为不含分母的方程,再用加减消元法或代入消元法求解即可.
解答 解:(1)$\left\{\begin{array}{l}2x-3y=6①\\ x=4+2y②\end{array}\right.$,把②代入①得,2(4+2y)-3y=6,解得y=-2,把y=-2代入②得,x=4-4=0,
故此方程组的解为$\left\{\begin{array}{l}x=0\\ y=-2\end{array}\right.$;
(2)$\left\{\begin{array}{l}3x+3y=0①\\ 3x+y=10②\end{array}\right.$,①-②得,2y=-10,解得y=-5,把y=-5代入②得,3x-5=10,解得x=5,
故方程组的解为$\left\{\begin{array}{l}x=5\\ y=-5\end{array}\right.$;
(3)$\left\{\begin{array}{l}4x-3y=5①\\ 2x-y=2②\end{array}\right.$,①-②×2得,-y=1,解得y=-1,把y=-1代入②得,2x+1=2,解得x=$\frac{1}{2}$,
故方程组的解为$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=-1\end{array}\right.$;
(4)原方程组可化为$\left\{\begin{array}{l}2x-3y=6①\\ 3x+2y=22②\end{array}\right.$,①×3-②×2得,-13y=-26,解得y=2,把y=2代入①得,2x-6=6,解得x=6,
故此方程组的解为$\left\{\begin{array}{l}x=6\\ y=2\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 1 | B. | ±1 | C. | $\sqrt{5}$ | D. | ±$\sqrt{5}$ |
| A. | 梯形 | B. | 五边形 | C. | 六边形 | D. | 圆 |
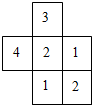 一个几何体由大小相同的小立方块组成,从上面看到的几何体的形状如图所示,其中小正方形中数字表示该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块组成,从上面看到的几何体的形状如图所示,其中小正方形中数字表示该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.