题目内容
已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根
有两个实数根![]() ,
,![]() 。
。
(1)求实数![]() 的取值范围;(4分)
的取值范围;(4分)
(2)是否存在实数![]() 使得
使得![]() ≥
≥![]() 成立?若存在,请求出
成立?若存在,请求出![]() 的值;若不存在,请说明理由。(6分)
的值;若不存在,请说明理由。(6分)
解:(1)∵原方程有两个实数根,
∴ ![]() ≥
≥![]() ∴
∴![]() ≥
≥![]() ∴
∴![]() ≥
≥![]() ,
,
∴![]() ≤
≤![]() .∴当
.∴当![]() ≤
≤![]() 时,原方程有两个实数根.
时,原方程有两个实数根.
(2)假设存在实数![]() 使得
使得![]() ≥
≥![]() 成立.
成立.
∵![]() ,
,![]() 是原方程的两根,
是原方程的两根,
∴![]() .由
.由![]() ≥
≥![]() ,
,
得![]() ≥
≥![]() .
.
∴![]() ≥
≥![]() ,整理得:
,整理得:![]() ≥
≥![]() ,
,
∴只有当![]() 时,上式才能成立. 又由(1)知
时,上式才能成立. 又由(1)知![]() ≤
≤![]() ,
,
∴不存在实数![]() 使得
使得![]() ≥
≥![]() 成立.
成立.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围;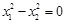 时,求
时,求 的一元二次方程
的一元二次方程 有两个实数根,求
有两个实数根,求 的取值范围及
的取值范围及 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求 的一元二次方程
的一元二次方程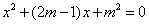 有两个实数根
有两个实数根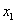 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求