题目内容
9.(1)解不等式:5x-12≤2(4x-3)(2)解不等式:5-2(x-3)≤x-1
(3)解不等式组$\left\{\begin{array}{l}{3(x+1)>5x+4①}\\{\frac{x-1}{2}≤\frac{2x-1}{3}②}\end{array}\right.$,并将解集在数轴上表示出来.
分析 去括号,移项,合并同类项,系数化成1即可.去括号,移项,合并同类项,系数化成1即可.首先解出两个不等式的解集,再根据大小小大中间找确定不等式组的解集.
解答 解:(1)5x-12≤2(4x-3),
5x-12≤8x-6,
5x-8x≤-6+12,
-3x≤6,
x≥-2
(2)5-2(x-3)≤x-1,
5-2x+6≤x-1,
-2x-x≤-1-5-6
-3x≤-12,
x≥4;
(3)$\left\{\begin{array}{l}{3(x+1)>5x+4①}\\{\frac{x-1}{2}≤\frac{2x-1}{3}②}\end{array}\right.$,
解不等式①得:x<-$\frac{1}{2}$,
解不等式②得x≥-1,
所以不等式组的解集为:-1≤x<-$\frac{1}{2}$,
在数轴上表示为: .
.
点评 此题主要考查了一元一次不等式组的解法,关键是掌握确定解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
14. 已知a,b在数轴上的位置如图所示,则a-b的结果的符号为( )
已知a,b在数轴上的位置如图所示,则a-b的结果的符号为( )
 已知a,b在数轴上的位置如图所示,则a-b的结果的符号为( )
已知a,b在数轴上的位置如图所示,则a-b的结果的符号为( )| A. | 正 | B. | 负 | C. | 0 | D. | 无法确定 |
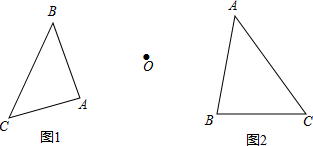 如图,已知△ABC,(1)图1中以点O为旋转中心顺时针旋转60°的图形.
如图,已知△ABC,(1)图1中以点O为旋转中心顺时针旋转60°的图形. 如图,在长28米,宽21米的矩形场地中间有横、竖三条道路,横、竖道路宽之比为3:2,三条道路的总面积为156平方米,求横、竖道路宽各多少米?(注:两条竖直的道路一样宽)
如图,在长28米,宽21米的矩形场地中间有横、竖三条道路,横、竖道路宽之比为3:2,三条道路的总面积为156平方米,求横、竖道路宽各多少米?(注:两条竖直的道路一样宽) 已知△ABC,在△ABC内求作一点P,使它到△ABC三个顶点的距离相等.
已知△ABC,在△ABC内求作一点P,使它到△ABC三个顶点的距离相等.