题目内容
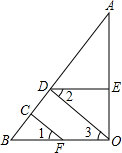如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2，请问：OD与AB垂直吗？试说明理由．
解：OD⊥AB．理由如下：
∵DE⊥AO，BO⊥AO（已知），
∴∠DEA=∠BOA=90°（垂直定义），
∴DE∥OB（同位角相等，两直线平行），
∴∠2=∠3（两直线平行，内错角相等），
∵∠1=∠2（已知），
∴∠1=∠3（等量代换），
∴OD∥FC（同位角相等，两直线平行），
∵FC⊥AB（已知），
∴OD⊥AB（等量代换）．
分析：首先由DE⊥AO，BO⊥AO，推出DE∥OB，得出∠2=∠3，再通过等量代换推出∠1=∠3，即可推出OD∥CF，最后由FC⊥AB，推出OD与AB垂直．
点评：本题主要考查平行线的判定与性质、垂直定义、等量代换，关键在于熟练掌握运用相关的性质定理，推出OD∥FC．
∵DE⊥AO，BO⊥AO（已知），
∴∠DEA=∠BOA=90°（垂直定义），
∴DE∥OB（同位角相等，两直线平行），
∴∠2=∠3（两直线平行，内错角相等），
∵∠1=∠2（已知），
∴∠1=∠3（等量代换），
∴OD∥FC（同位角相等，两直线平行），
∵FC⊥AB（已知），
∴OD⊥AB（等量代换）．
分析：首先由DE⊥AO，BO⊥AO，推出DE∥OB，得出∠2=∠3，再通过等量代换推出∠1=∠3，即可推出OD∥CF，最后由FC⊥AB，推出OD与AB垂直．
点评：本题主要考查平行线的判定与性质、垂直定义、等量代换，关键在于熟练掌握运用相关的性质定理，推出OD∥FC．
练习册系列答案
步步高达标卷系列答案
相关题目
23、如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2，找出图中互相平行的线，并加以说明．
28、如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2．
如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于C，∠1=∠2．